题目内容
已知
+
+
=
.求A、B、C的值.
| A |
| x-1 |
| B |
| x+1 |
| C |
| x-2 |
| 3x-9 |
| (x2-1)(x-2) |
考点:分式的加减法
专题:计算题
分析:已知等式左边通分并利用同分母分式的加法法则变形,利用多项式相等的条件即可确定出A,B,C的值.
解答:解:
+
+
=
=
,
∴(x2-x-2)A+(x2-3x+2)B+(x2-1)C=(A+B+C)x2-(A+3B+C)x-2A+2B-C=3x-9,
∴A+B+C=0,A+3B+C=-3,-2A+2B-C=-9,
解得:A=
,B=-
,C=-3.
| A |
| x-1 |
| B |
| x+1 |
| C |
| x-2 |
| A(x+1)(x-2)+B(x-1)(x-2)+C(x+1)(x-1) |
| (x2-1)(x-2) |
| 3x-9 |
| (x2-1)(x-2) |
∴(x2-x-2)A+(x2-3x+2)B+(x2-1)C=(A+B+C)x2-(A+3B+C)x-2A+2B-C=3x-9,
∴A+B+C=0,A+3B+C=-3,-2A+2B-C=-9,
解得:A=
| 9 |
| 2 |
| 3 |
| 2 |
点评:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
某商品原价269元,经连续两次降价后,售价为256元.设平均每次降价的百分率为x,则可列方程为
( )
( )
| A、269(1+x)2=256 |
| B、269(1-x)2=256 |
| C、256(1-x)2=269 |
| D、269-269x2=256 |
 如图所示,已知直角梯形ABCD中,AD∥BC,∠C=∠D=90°,以AB为直径的⊙O与CD相切于P,若AD=m,BC=n,CD=a.求证:
如图所示,已知直角梯形ABCD中,AD∥BC,∠C=∠D=90°,以AB为直径的⊙O与CD相切于P,若AD=m,BC=n,CD=a.求证: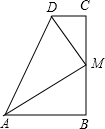 已知:如图,四边形ABCD中,AB∥CD,AM平分∠DAB,DM平分∠ADC,点M恰在BC上.
已知:如图,四边形ABCD中,AB∥CD,AM平分∠DAB,DM平分∠ADC,点M恰在BC上. 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG. 如图,在?ABCD中,BC=2AB,点M是AD的中点,CE⊥AB于E,如果∠AEM=50°,求∠B的度数.
如图,在?ABCD中,BC=2AB,点M是AD的中点,CE⊥AB于E,如果∠AEM=50°,求∠B的度数. 我们在学习实数时,画了这样一个图:即以数轴上1个单位长的线段为边作正方形,再以原点0为圆心,正方形的对角线OA长为半径画弧.交数轴于点B、C.请根据图形填空.
我们在学习实数时,画了这样一个图:即以数轴上1个单位长的线段为边作正方形,再以原点0为圆心,正方形的对角线OA长为半径画弧.交数轴于点B、C.请根据图形填空.