题目内容
 如图,在四边形ABCD中,AB=AD=2,∠A=60°,BC=2
如图,在四边形ABCD中,AB=AD=2,∠A=60°,BC=2| 5 |
(1)求∠ADC的度数.
(2)求四边形ABCD的面积.
考点:等边三角形的判定与性质,勾股定理的逆定理
专题:
分析:(1)连接BD,根据AB=AD=2,∠A=60°,得出△ABD是等边三角形,求得BD=2,然后根据勾股定理的逆定理判断三角形BDC是直角三角形,从而求得∠ADC=150°;
(2)根据四边形的面积等于三角形ABD和三角形BCD的和即可求得;
(2)根据四边形的面积等于三角形ABD和三角形BCD的和即可求得;
解答:解:(1)连接BD,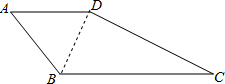
∵AB=AD=2,∠A=60°,
∴△ABD是等边三角形,
∴BD=2,∠ADB=60°,
∵BC=2
,CD=4,
则BD2+CD2=22+42=20,BC2=(2
)2=20,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=150°;
(2)S=S△ABD+S△BDC=
AD•
AD+
BD•DC=
×2×
×2+
×2×4=4+2
.

∵AB=AD=2,∠A=60°,
∴△ABD是等边三角形,
∴BD=2,∠ADB=60°,
∵BC=2
| 5 |
则BD2+CD2=22+42=20,BC2=(2
| 5 |
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=150°;
(2)S=S△ABD+S△BDC=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
点评:本题考查了等边三角形的判定和性质,直角三角形的判定和性质,把不规则的图形转化成规则的三角形求得面积等.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
该列数据0,0,1,1,1,2,3的众数是( )
| A、2 | B、0 | C、1 | D、3 |
已知一个样本:26,28,25,29,31,27,30,32,28,26,32,29,28,24,26,27,30,那么下列哪一组的频数为3( )
| A、24.5~26.5 |
| B、26.5~28.5 |
| C、28.5~30.5 |
| D、30.5~32.5 |
某商品原价269元,经连续两次降价后,售价为256元.设平均每次降价的百分率为x,则可列方程为
( )
( )
| A、269(1+x)2=256 |
| B、269(1-x)2=256 |
| C、256(1-x)2=269 |
| D、269-269x2=256 |
 作出下列图形关于直线l对称的图形.
作出下列图形关于直线l对称的图形.
 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG.