题目内容
12. 如图,AB是⊙O直径,C、D是弧AB的三等分点,P为直径AB上一点,若AB=12,则图中阴影部分的面积为6π.
如图,AB是⊙O直径,C、D是弧AB的三等分点,P为直径AB上一点,若AB=12,则图中阴影部分的面积为6π.
分析 连接OC、OD、AD,求出阴影部分的面积=扇形COD的面积,求出扇形的面积即可.
解答 解: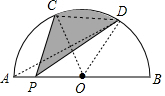
连接OC、OD、AD,
∵C、D是弧AB的三等分点,
∴$\widehat{AC}$=$\widehat{BD}$,
∴∠CDA=∠BAD,
∴CD∥AB,
∴S△PCD=S△COD,
∴阴影部分的面积和扇形OCD的面积相等,
∵C、D是弧AB的三等分点,直径AB=12,
∴∠COD=60°,OC=6,
∴阴影部分的面积=$\frac{60π×{6}^{2}}{360}$=6π,
故答案为:6π.
点评 本题考查了圆周角定理,扇形的面积计算,能求出阴影部分的面积=扇形COD的面积是解此题的关键,也可以直接阴影部分的面积=半圆面积的$\frac{1}{3}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.甲、乙、丙三名射箭运动员在某次测试中各射箭8次,三人的测试成绩如表:
s2甲、s2乙、s2丙分别表示甲、乙、丙三名运动员这次测试成绩的方差,下面各式中正确的是( )
| 甲的成绩 | 乙的成绩 | 丙的成绩 | ||||||||||||||
| 环数 | 7 | 8 | 9 | 10 | 环数 | 7 | 8 | 9 | 10 | 环数 | 7 | 8 | 9 | 10 | ||
| 频数 | 1 | 3 | 3 | 1 | 频数 | 2 | 2 | 2 | 2 | 频数 | 3 | 1 | 1 | 3 | ||
| A. | s2甲>s2乙>s2丙 | B. | s2乙>s2甲>s2丙 | C. | s2丙>s2甲>s2乙 | D. | s2丙>s2乙>s2甲 |
17. 如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
 如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )| A. | 9π | B. | 10π | C. | 11π | D. | 12π |
11.某商店购进了A,B两种家用电器,相关信息如下表:
已知用6000元购进的A种电器件数与用5000元购进的B种电器件数相同.
(1)求表中m的值.
(2)由于A,B两种家用电器热销,该商店计划用不超过23000元的资金再购进A,B两种电器总件数共20件,且获利不少于13300元.请问:有几种进货方案?哪一种方案才能获得最大利润?最大利润是多少?
| 家用电器 | 进价(元/件) | 售价(元/件) |
| A | m+200 | 1800 |
| B | m | 1700 |
(1)求表中m的值.
(2)由于A,B两种家用电器热销,该商店计划用不超过23000元的资金再购进A,B两种电器总件数共20件,且获利不少于13300元.请问:有几种进货方案?哪一种方案才能获得最大利润?最大利润是多少?
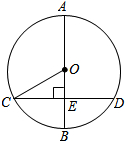 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CO.如果CO=2cm,∠COE=60°,那么劣弧$\widehat{CD}$的长是$\frac{4}{3}$πcm.
如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CO.如果CO=2cm,∠COE=60°,那么劣弧$\widehat{CD}$的长是$\frac{4}{3}$πcm. 如图,抛物线y=$\frac{1}{4}$x2+bx+c与两轴交于点A(2,0),点B(0,-$\frac{5}{2}$),直线y=kx+$\frac{3}{2}$,过点A与y轴交于点C,与抛物线的另一个交点是D点.
如图,抛物线y=$\frac{1}{4}$x2+bx+c与两轴交于点A(2,0),点B(0,-$\frac{5}{2}$),直线y=kx+$\frac{3}{2}$,过点A与y轴交于点C,与抛物线的另一个交点是D点.
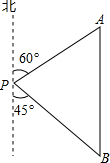 五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果保留根号)
五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果保留根号)