题目内容
6. 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.(1)求证:BD=AE.
(2)若线段AD=5,AB=17,求线段ED的长.
分析 (1)利用等腰直角三角形的性质,证明△ACE≌△BCD,即可解答;
(2)由AD=5,AB=17,求得BD=17-5=12,根据△ABC是等腰直角三角形,得到∠B=45°,由(1)可知△ACE≌△BCD,得到∠EAC=∠B=45°,AE=BD=7,
进而∠EAD=90°,根据勾股定理即可解答.
解答 解:(1)∵△ABC和△ECD都是等腰直角三角形,
∴AC=BC,CD=CE,
∵∠ACD=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CD=CE}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴BD=AE.
(2)∵AD=5,AB=17,
∴BD=17-5=12,
∵△ABC是等腰直角三角形
∴∠B=45°由(1)可知△ACE≌△BCD
∴∠EAC=∠B=45°,AE=BD=7,
∴∠EAD=90°,
∴ED=$\sqrt{A{E^2}+A{D^2}}=\sqrt{{{12}^2}+{5^2}}=13$.
点评 本题考查了全等三角形的性质与判定、等腰直角三角形的性质,解决本题的关键是利用等腰直角三角形的性质证明△ACE≌△BCD.

练习册系列答案
相关题目
8.正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.

(1)填写下表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … | 2(n+1) |
14. 一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
 一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )| A. | 不能 | B. | 带① | C. | 带② | D. | 带③ |
11.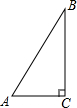 如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )
如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )
 如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )
如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )| A. | 3 | B. | 9 | C. | 10 | D. | 15 |
 如图所示,在△ABC中,∠BAC=90°,AB=AC,DE过A点,且CE⊥ED,BD⊥ED.若CE=2,BD=4,求ED的长.
如图所示,在△ABC中,∠BAC=90°,AB=AC,DE过A点,且CE⊥ED,BD⊥ED.若CE=2,BD=4,求ED的长. 已知:如图,在△ABC中,∠A=30°,∠B=60°
已知:如图,在△ABC中,∠A=30°,∠B=60° 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,10),点B在第一象限内.D为OC的中点.
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,10),点B在第一象限内.D为OC的中点.