题目内容
17.若α、β是一元二次方程x2+2x-6=0的两根,求$\frac{1}{α}$+$\frac{1}{β}$和α2+β2的值.分析 根据根与系数的关系得到α+β=-2,αβ=-6,再把代数式$\frac{1}{α}$+$\frac{1}{β}$=$\frac{α+β}{αβ}$,α2+β2=(α+β)2-2αβ,然后利用整体代入的方法计算.
解答 解:∵α、β是一元二次方程x2+2x-6=0的两根,
∴α+β=-2,αβ=-6,
∴$\frac{1}{α}$+$\frac{1}{β}$=$\frac{α+β}{αβ}$=$\frac{1}{3}$,
α2+β2=(α+β)2-2αβ=4+12=16.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
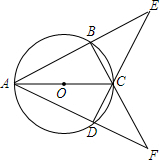 如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.
如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.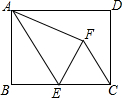 矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$.
矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$. 在平面直角坐标系中,△ABC的位置如图所示,△DEF的顶点坐标分别为D(0,-1)、E(-4,-3)、F(-1.-3).
在平面直角坐标系中,△ABC的位置如图所示,△DEF的顶点坐标分别为D(0,-1)、E(-4,-3)、F(-1.-3).