Question

（本题7分）已知关于的方程.

（1）求证：无论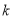取任何实数值，方程总有实数根；

（2）若等腰三角形ABC的一边长，另两边长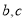恰好是这个方程的两个根，求此三角形的周长.

Answer 1

（1）证明见解析；

（2）三角形的周长为16或22；

【解析】

试题分析：（1）由一元二次方程根的判别式，当△≥0时，方程有两个实数根，所以只需证明△≥0即可．

（2）先求出方程的两根x1=3k-1，x2=2，则可设b=2k，c=k+1，然后讨论：当a、b为腰、当b、c为腰、当a、c为腰分别求出边长，但要满足三角形三边的关系，最后计算周长即可．

试题解析：△=[-（3k+1）]2-4×1×（2k2+2k），

=k2-2k+1，

=（k-1）2，

∵无论k取什么实数值，（k-1）2≥0，

∴△≥0，

所以无论k取什么实数值，方程总有实数根；

（2）x2-（3k+1）x+2k2+2k=0，

因式分解得：（x-2k）（x-k-1）=0，

解得：x1=2k，x2=k+1，

∵b，c恰好是这个方程的两个实数根，设b=2k，c=k+1，

当a、b为腰，则a=b=6，而a+b＞c，a-b＜c，所以三角形的周长为：6+6+4=16；

当b、c为腰，则k+1=2k，解得k=1，

∴b=c=2，因为6，2，2不构成三角形，∴所以这种情况不成立；

当a、c为腰 k+1=6 则k=5，

∴b=10，

∴三角形的周长为：6+6+10=22

综上，三角形的周长为16或22；

考点：1、根的判别式；2、等腰三角形的性质

考点分析： 考点1：一元二次方程 定义：
只含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程。

一元二次方程的一般形式：
它的特征是：等式左边是一个关于未知数x的二次多项式，等式右边是零，其中 ax²叫做二次项，a叫做二次项系数；bx叫做一次项，b叫做一次项系数；c叫做常数项。 试题属性

• 题型：
• 难度：
• 考核：
• 年级：