题目内容
(本题12分)已知,如图,在平面直角坐标系中,点A、B的横坐标恰好是方程 的解,点C的纵坐标恰好是方程
的解,点C的纵坐标恰好是方程 的解,点P从C点出发沿y轴正方向以1个单位/秒的速度向上运动,连PA、PB,D为AC的中点.
的解,点P从C点出发沿y轴正方向以1个单位/秒的速度向上运动,连PA、PB,D为AC的中点.

1)求直线BC的解析式;
2)设点P运动的时间为t秒,问:当t为何值时,DP与DB垂直且相等?
3)如图2,若PA=AB,在第一象限内有一动点Q,连QA、QB、QP,且∠PQA=60°,问:当Q在第一象限内运动时,∠APQ+∠ABQ的度数和是否会发生改变?若不变,请说明理由并求其值.
(1)直线BC的解析式为y=-x+2;
(2)当t=2秒,即CP=OC时,DP与DB垂直且相等;
(3)当Q在第一象限内运动时,∠APQ+∠ABQ的度数和不会发生改变, 为180°.理由见解析;
【解析】
试题分析:(1)解方程可求出A(-2,0),B(2,0),C(0,2),再设直线BC的解析式为y=kx+b,将B、C两点的坐标代入,用待定系数法即可求出直线BC的解析式;
(2)当t=2秒,即CP=OC时,DP与DB垂直且相等.为此,作DM⊥x轴于点M,作DN⊥y轴于点N,根据等腰直角三角形及角平分线的性质,利用SAS证明△PCD≌△BOD,则DP=DB,∠PDC=∠BDO,进而得到∠BDP=∠ODC=90°,即DP⊥DB;
(3)在QA上截取QS=QP,连接PS,利用∠PQA=60°,得出△QSP是等边三角形,进而得出△APS≌△BPQ,从而得出∠APQ+∠ABQ=60°+∠APQ+∠PAS=180°得出答案.
试题解析:(1)解方程x2-4=0得,x1=-2,x2=2,所以A(-2,0)、B(2,0),
解方程x2-4x+4=0得x1=x2=2,所以C(0,2),
设直线BC的解析式为y=kx+b,将B、C两点的坐标代入,
得 ,解得
,解得 ,
,
∴直线BC的解析式为y=-x+2;
(2)当t=2秒,即CP=OC时,DP与DB垂直且相等.理由如下:
如图1,连接OD,作DM⊥x轴于点M,作DN⊥y轴于点N,

∵A(-2,0),C(0,2),
∴△OAC是等腰直角三角形,
∵D为AC的中点,
∴OD平分∠AOC,OD=DC= AC,
AC,
∴DM=DN=OM=ON=m.
在△PCD与△BOD中,
 ,
,
∴△PCD≌△BOD (SAS),
∴DP=DB,∠PDC=∠BDO,
∴∠BDP=∠ODC=90°,
即DP⊥DB;
(3)当Q在第一象限内运动时,∠APQ+∠ABQ的度数和不会发生改变.理由如下:
如图2,在QA上截取QS=QP,连接PS,

∵∠PQA=60°,
∴△QSP是等边三角形,
∴PS=PQ,∠SPQ=60°,
∵PO是AB的垂直平分线,
∴PA=PB,而PA=AB,
∴PA=PB=AB,
∴∠APB=∠ABP=60°,
∴∠APS=∠BPQ,
∴△APS≌△BPQ(SAS),
∴∠PAS=∠PBQ,
∴∠APQ+∠ABQ
=∠APQ+(∠ABP+∠PBQ)
=60°+(∠APQ+∠PBQ)
=60°+(∠APQ+∠PAS)=60°+120°=180°;
考点:1、待定系数法;2、全等三角形的判定与性质;3、等腰直角三角形的判定与性质;4、等边三角形的性质与判定
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案(10分)张明、王成两位同学初二一学年10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示:利用图中提供的信息,解答下列问题.
(1)完成下表
姓名 | 平均成绩 | 中位数 | 众数 | 方差(S2) |
张明 | 80 | 80 | ||
王成 | 260 |
(2)如果将90分以上(含90分)的成绩视为A等,则获得成绩为A等多的同学是 ;
(3)根据图表信息,请你对这位两同学各提一条不超过20个字的学习建议,并说明提出建议的原因.

 的一元二次方程
的一元二次方程 的一个根是1,则
的一个根是1,则 = .
= . 的方程
的方程 .
.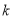 取任何实数值,方程总有实数根;
取任何实数值,方程总有实数根; ,另两边长
,另两边长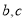 恰好是这个方程的两个根,求此三角形的周长.
恰好是这个方程的两个根,求此三角形的周长. 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 .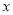 的一元二次方程
的一元二次方程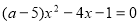 有实数根,则
有实数根,则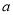 满足条件是( )
满足条件是( )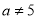 B、
B、 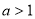 且
且 C、.
C、. 且
且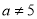 D、
D、