��Ŀ����
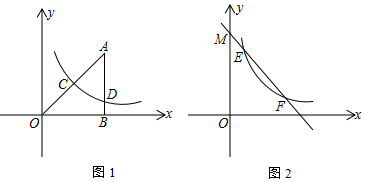
19�����Ǹ������¶��壺��һ���ı�����һ��Խǻ��������Խ�֮��Ϊ180�㣩���������ı���ΪԲ���ı��Σ���1���������⣺��ƽ���ı��Ρ����Ρ����Ρ��������У�����Ϊ����Բ���ı��ε��о��Σ������Σ�
��2������̽������ͼ?�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������ADB=��ACB�����ı���ABCD��Բ���ı�������˵�����ɣ�С������˼�����ж��ı���ABCD��Բ���ı��Σ������������̽��˼·����֤����AOD�ס�BOC���õ�����ʽ$\frac{OA}{OB}$=$\frac{OD}{OC}$����֤����AOB�ס�DOC���ó���Ӧ����ȣ������ı����ڽǺͶ������ó�һ��Խǻ������������С��д��������̣�
��3�����������������������������۵ľ����֪ʶ������⣮��ͼ?���ı���ABCD�У�AD��BD��AC��BC��AB��DC���ӳ����ཻ�ڵ�E��BE=BD��AB=5��AD=3����CE�ij���

���� ��1������Բ���ı��εĶ���ֱ���жϼ��ɣ�
��2�����жϳ���AOD�ס�BOC��������AOB�ס�DOC���ɵó���ADB+��ABC=��DCB+��DAB=180�㼴�ɣ�
��3�����жϳ���BCE=��DAB�������ó���BEC�ס�DEA������$\frac{EC}{AE}=\frac{BC}{AD}$����Ϊ��ʾ��BC=$\sqrt{25-{x}^{2}}$
�����BD=4��EA=9���������ʽ�������EC��
��� �⣺��1���߾��κ������ε��ĸ��ڽǶ���90�㣬
����κ������ε�����Խǵĺ�Ϊ180�㣬
����Σ���������Բ���ı��Σ�
�ʴ��ǣ����Σ������Σ�
��2��֤�����ߡ�ADB=��ACB����AOD=��BOC��
���DAO=��CBO��
���AOD�ס�BOC��
��$\frac{OA}{OB}=\frac{OD}{OC}$���֡ߡ�AOB=��DOC��
���AOB�ס�DOC��
���OAB=��ODC����OBA=��OCD��
���ADB+��ODC+��OBA+��OBC=��ACB+��OAB+��OCD+��OAD=180�㣬
����ADB+��ABC=��DCB+��DAB=180�㣮
���ı���ABCD��Բ���ı��Σ�
��3����ͼ?����AD��BD��AC��BC��
���ADB=��ACB=90�㣬
���ı���ABCD��Բ���ı��Σ�
���Ͽɵã���DAB+��DCB=��ADC+��ABC=180�㣬��BDC=��BAC��
�֡�BE=BD��
���BED=��BDC=��BAC��
��AC=EC��
�֡ߡ�BCE+��DCB=180�㣬
���BCE=��DAB��
�֡�BEC=��DEA��
���BEC�ס�DEA��
��$\frac{EC}{AE}=\frac{BC}{AD}$��
��AC=EC=x����BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{25-{x}^{2}}$
BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=4��
��EA=5+4=9��
��$\frac{\sqrt{25-{x}^{2}}}{3}=\frac{x}{9}$����ã�x=$\frac{3\sqrt{10}}{2}$��
����CE=$\frac{3\sqrt{10}}{2}$��
���� �������������ۺ��⣬��Ҫ�������¶���������Ӧ�ã����������ε��ж������ʣ����ɶ������⣨2���Ĺؼ����жϳ���AOB�ס�DOC���⣨3���Ĺؼ����жϳ���BEC�ס�DEA����һ���е��Ѷȵ��п������⣮

| A�� | ��-a+b����-a-b��=a2-b2 | B�� | ��-a-b��2=a2+b2+2ab | C�� | ��-a+b��2=a2+b2-2ab | D�� | ��-a-b����a+b��=a2-b2 |
| A�� | x3x2=x5 | B�� | -x2-x2=-2x2 | C�� | ��-2x��2=-4x2 | D�� | ��-2x����-3x2��=6x3 |

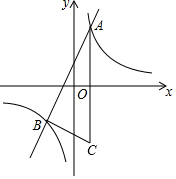 ��֪����������y1=$\frac{k}{x}$��ͼ����һ�κ���y2=ax+b��ͼ���ڵ�A��1��4���͵�B��-2��m������C���A����x��Գƣ�
��֪����������y1=$\frac{k}{x}$��ͼ����һ�κ���y2=ax+b��ͼ���ڵ�A��1��4���͵�B��-2��m������C���A����x��Գƣ�