题目内容
已知：2+
=22×
，3+
=32×
，4+
=42×
，…，观察规律填空：
（1）请写出下一个等式： ．
（2）用含n的代数式表示这个规律： ．
（3）若10+
=102×
（a、b为正整数），则a+b ．
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 8 |
| 3 |
| 8 |
| 4 |
| 15 |
| 4 |
| 15 |
（1）请写出下一个等式：
（2）用含n的代数式表示这个规律：
（3）若10+
| a |
| b |
| a |
| b |
考点：规律型：数字的变化类
专题：
分析：由已知算式可知：等号左边第一个加数的数字和第二个加数分数的分子相同，分母是分子的平方减去1，等号的右边是第一个加数的平方乘第二个加数；
（1）利用以上规律可以接着写出5+
=52×
；
（2）进一步利用（1）的规律表示出即可；
（3）利用（2）的规律求出a、b即可．
（1）利用以上规律可以接着写出5+
| 5 |
| 24 |
| 5 |
| 24 |
（2）进一步利用（1）的规律表示出即可；
（3）利用（2）的规律求出a、b即可．
解答：解：（1）5+
=52×
；
（2）n+
=n2×
；
（3）若10+
=102×
（a、b为正整数），
所以a=10，b=102-1=99
则a+b=10+99=109．
故答案为：（1）5+
=52×
；（2）n+
=n2×
；（3）109．
| 5 |
| 24 |
| 5 |
| 24 |
（2）n+
| n |
| n2-1 |
| n |
| n2-1 |
（3）若10+
| a |
| b |
| a |
| b |
所以a=10，b=102-1=99
则a+b=10+99=109．
故答案为：（1）5+
| 5 |
| 24 |
| 5 |
| 24 |
| n |
| n2-1 |
| n |
| n2-1 |
点评：此题主要考查算式的变化规律，对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．通过分析找到各部分的变化规律后直接利用规律求解．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
若|2-a|+
=0，则a+b的值是（ ）
| 3+b |
| A、2 | B、0 | C、1 | D、-1 |
如图，正方形ABCD中，AB=4cm，点M、P分别从D、B两点同时出发，以1.5cm/s、1cm/s的速度沿DA、BC运动；点N从A点以3cm/s的速度也同时出发，沿AB、BC运动，当点N到达点C时，点N、M、P同时停止运动，设运动时间为t（s）；△MNP的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（ ）
若x与2互为相反数，则x的值是（ ）
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
如图是8×9的网格，网格中每个小正方形的边长均为1，线段AB的端点在小正方形的顶点上．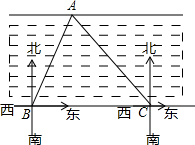
如图，某施工单位为测得某河段的宽度，测量员先在河对岸边取一点A，再在河这边沿河边取两点B、C，在点B处测得A在北偏东30°方向上，在点C处测得点A在西北方向上，量得BC长为400米，请你求出该河段的宽度．（结果保留根号）
已知：如图，在?ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC．