题目内容
17.(1)解不等式$x≤3-\frac{1}{2}x<5$(2)解不等式组$\left\{{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3({x-1})<8-x}\end{array}}\right.$,并写出该不等式组的整数解.
分析 (1)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后求得不等式组的整数解即可.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{3-\frac{1}{2}x≥x…①}\\{3-\frac{1}{2}x<5…②}\end{array}\right.$,
解①得x≤2,
解②得x>-4.
则不等式组的解集是:-4<x≤2;
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1…①}\\{1-3(x-1)<8-x…②}\end{array}\right.$,
解①得x≤1,
解②得x>-2.
则不等式组的解集是:-2<x≤1.
整数解是-1,0,1.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
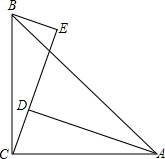 如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.
如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.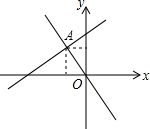 如图,函数y=-2x和y=kx+4的图象相交于点A(m,3),则关于的x不等式kx+4+2x≥0的解集为x≥-1.5.
如图,函数y=-2x和y=kx+4的图象相交于点A(m,3),则关于的x不等式kx+4+2x≥0的解集为x≥-1.5.