题目内容
3.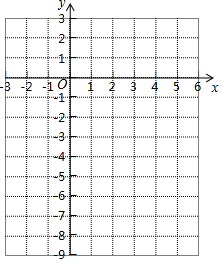 已知抛物线C1:y=ax2-4ax-5(a>0).
已知抛物线C1:y=ax2-4ax-5(a>0).(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
分析 (1)将a=1代入解析式,即可求得抛物线与x轴交点;
(2)①化简抛物线解析式,即可求得两个定点的横坐标,即可解题;
②根据抛物线翻折理论即可解题;
(3)根据(2)中抛物线C2解析式,分类讨论y=2或-2,即可解题;
解答 解:(1)当a=1时,抛物线解析式为y=x2-4x-5=(x-2)2-9,
∴对称轴为x=2;
∴当y=0时,x-2=3或-3,即x=-1或5;
∴抛物线与x轴的交点坐标为(-1,0)或(5,0);
(2)①抛物线C1解析式为:y=ax2-4ax-5,
整理得:y=ax(x-4)-5;
∵当ax(x-4)=0时,y恒定为-5;
∴抛物线C1一定经过两个定点(0,-5),(4,-5);
②这两个点连线为y=-5;
将抛物线C1沿y=-5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;
∴抛物线C2解析式为:y=-ax2+4ax-5,
(3)抛物线C2的顶点到x轴的距离为2,
则x=2时,y=2或者-2;
当y=2时,2=-4a+8a-5,解得,a=$\frac{7}{4}$;
当y=-2时,-2=-4a+8a-5,解得,a=$\frac{3}{4}$;
∴a=$\frac{7}{4}$或$\frac{3}{4}$;
点评 本题考查了代入法求抛物线解析式的方法,考查了抛物线翻折后对称轴不变的原理,考查了抛物线顶点的求解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11. 如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
 如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2 | D. | 1 |
18.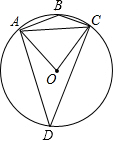 如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
 如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )| A. | 30° | B. | 50° | C. | 40° | D. | 45° |
13.若将半径为12cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( )
| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
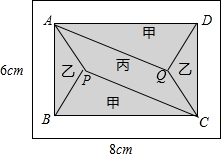 小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示. 如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC=27°.
如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC=27°.