题目内容
12. 如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC=27°.
如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC=27°.
分析 根据菱形的性质得到∠ACB=$\frac{1}{2}$∠DCB=$\frac{1}{2}$(180°-∠D)=51°,根据圆内接四边形的性质得到∠AEB=∠D=78°,由三角形的外角的性质即可得到结论.
解答 解:∵四边形ABCD是菱形,∠D=78°,
∴∠ACB=$\frac{1}{2}$∠DCB=$\frac{1}{2}$(180°-∠D)=51°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=78°,
∴∠EAC=∠AEB-∠ACE=27°,
故答案为:27.
点评 本题考查了菱形的性质,三角形的外角的性质,圆内接四边形的性质,熟练掌握菱形的性质是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
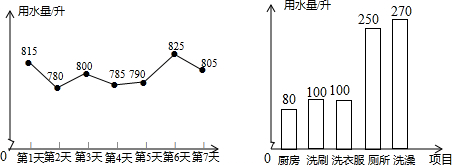
2.某地连续十天的最高气温统计如表:
则这种数据的中位数,众数,平均数分别是( )
| 最高气温(度) | 22 | 23 | 24 | 25 |
| 天 数 | 1 | 4 | 2 | 3 |
| A. | 23.5,23,23.7 | B. | 23,24,23.5 | C. | 24,23.5,25.5 | D. | 23.5,23,23.5 |
7.数据6,5,7.5,8.6,7,6的众数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
17.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
4.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.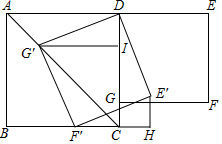 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )| A. | $\sqrt{2}$$+\sqrt{6}$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{3}+\sqrt{2}$ | D. | $\sqrt{3}+\sqrt{6}$ |
 已知抛物线C1:y=ax2-4ax-5(a>0).
已知抛物线C1:y=ax2-4ax-5(a>0).