题目内容
20．
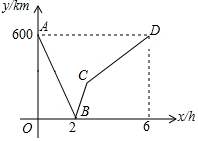一列快车从甲驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，匀速行驶，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的关系，根据图象进行以下探究：（1）甲、乙两地之间的距离为600 km；
（2）两车同时出发后经2h相遇；
（3）请直接写出图中点D所表示的实际意义；
（4）求慢车和快车的速度；
（5）请通过计算说明图中点C所表示的实际意义．
分析 （1）根据坐标系中A点纵坐标为600，得出甲乙两地距离即可；
（2）根据图象即可得到结论；
（3）根据两车相距600km，则点D即是慢车到达甲地；
（4）根据图中D点坐标即可得出慢车速度，进而利用B点坐标得出快车速度；
（5）利用图象中横纵坐标的意义得出C点的实际意义；
解答 解：（1）∵图中的折线表示y与x之间的函数关系，
∴坐标系中A点纵坐标即为两地距离，即600km，
故答案为：600；
（2）由函数图象，得图中点B的实际意义是：当慢车行驶42h时，慢车和快车相遇，
故答案为：2；
（3）图中点D的实际意义是：慢车行驶6h到达甲地
（4）由（3）可得慢车6h的行程为600km，
所以速度为600÷6=100（km/h）
∵两车出发后经2h 相遇．
∴快车速度为600÷2-100=200（km/h）
（5）∵快车速度为200km/h
∴$\frac{600}{200}$=3（h）
此时慢车走了100×3=300（km）
∴图中点C的实际意义是快车行驶3h到达乙地，此时慢车行驶了300km（或此时慢车离甲地还有300km）（10分）
点评 本题考查了一次函数的应用，主要利用了路程、时间、速度三者之间的关系，利用图象得出正确信息是解题关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
15．
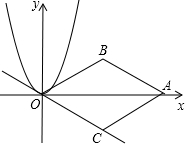如图，在平面直角坐标系中，点A（4$\sqrt{3}$，0）是x轴上一点，以OA为对角线作菱形OBAC，使得∠BOC=60°，现将抛物线y=x2沿直线OC平移到y=a（x-m）2+h，则当抛物线与菱形的AB边有公共点时，则m的取值范围是（ ）
如图，在平面直角坐标系中，点A（4$\sqrt{3}$，0）是x轴上一点，以OA为对角线作菱形OBAC，使得∠BOC=60°，现将抛物线y=x2沿直线OC平移到y=a（x-m）2+h，则当抛物线与菱形的AB边有公共点时，则m的取值范围是（ ）| A． | $\sqrt{3}$≤m≤3$\sqrt{3}$ | B． | 3$\sqrt{3}$≤m≤$\frac{10}{3}$$\sqrt{3}$ | C． | $\frac{10}{3}$$\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ | D． | $\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ |
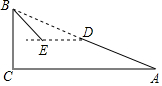如图，斜坡AB长130米，坡度i=1：2.4，BC⊥AC，