题目内容
1．按要求完成下列各小题：（1）计算：（$\frac{{x}^{2}}{5x}$-$\frac{{y}^{2}}{5x}$）•$\frac{x}{x+y}$；
（2）解方程：$\frac{2}{x-7}$+$\frac{5}{x}$=0．
分析 （1）原式括号中利用同分母分式的减法法则计算，约分即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=$\frac{（x+y）（x-y）}{5x}$•$\frac{x}{x+y}$=$\frac{x-y}{5}$；
（2）去分母得：2x+5x-35=0，
解得：x=5，
经检验，x=5是原分式方程的解．
点评 此题考查了解分式方程，以及分式的混合运算，解分式方程利用了转化的思想，解分式方程注意要检验．
练习册系列答案
出彩同步大试卷系列答案
相关题目
如图，用一个半径为30cm扇形铁皮，制作一个无底的圆锥（不计损耗），经测量圆锥的底面半径r为10cm，则扇形铁皮的面积为300πcm2．（结果保留π）
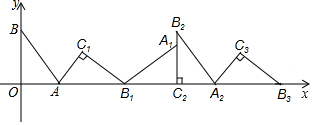
如图所示，以直角三角形ABC的三边向外作正方形，其面积分别为S1，S2，S3，且S1=4，S2=8，则S3=12．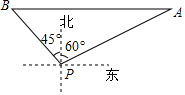
如图，一艘轮船位于灯塔P北偏东60°方向上，距离灯塔40海里的A处，它向西航行多少海里到达灯塔P北偏西45°方向上的B处．（参考数据：$\sqrt{3}$≈1.732，结果精确到0.1）
如图，已知点A，B，C在同一平面内，按要求完成下列各小题．