题目内容
4.计算:(1)3$\sqrt{20}$-$\sqrt{45}$+$\sqrt{\frac{1}{5}}$
(2)$\frac{\sqrt{48}-\sqrt{75}}{\sqrt{3}}+3$
(3)($\sqrt{3}-1$)2-(3+2$\sqrt{2}$)(3-2$\sqrt{2}$)
(4)求x的值:3(x+1)2=48.
分析 (1)根据二次根式的计算解答即可;
(2)根据二次根式的计算解答;
(3)根据完全平方公式和平方差公式进行计算;
(4)根据平方根的定义解答即可.
解答 解:(1)3$\sqrt{20}$-$\sqrt{45}$+$\sqrt{\frac{1}{5}}$=$12\sqrt{5}-3\sqrt{5}+\frac{\sqrt{5}}{5}=\frac{46}{5}\sqrt{5}$;
(2)$\frac{\sqrt{48}-\sqrt{75}}{\sqrt{3}}+3$=$\frac{4\sqrt{3}-5\sqrt{3}}{\sqrt{3}}+3=-1+3=2$;
(3)($\sqrt{3}-1$)2-(3+2$\sqrt{2}$)(3-2$\sqrt{2}$)=$4-2\sqrt{3}-9+8=3-2\sqrt{3}$;
(4)3(x+1)2=48,
x+1=±4,
x=3或x=-5.
点评 此题考查二次根式的计算,关键是根据二次根式的化简进行计算.

练习册系列答案
相关题目
12.“十•一”黄金周期间,一农家花博园统计了10月1日至10月6日每天参观的人数及变化,如表(正数表示比前一天多的人数,负数表示比前一天少的人数):
(1)若10月1日的游客人数记为a人,请用a的代数式表示10月3日的游客人数(直接在横线上写出结果):a+450.
(2)若a=1000,花博园门票每人20元,问10月1日至6日期间游客人数最多一天门票收入多少元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 |
| 人数 | a | -100 | +550 | -200 | +600 | -300 |
(2)若a=1000,花博园门票每人20元,问10月1日至6日期间游客人数最多一天门票收入多少元?
19.若点A(2,m)在x轴上,则点B(m-1,m+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )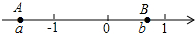
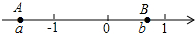
| A. | a+b<0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
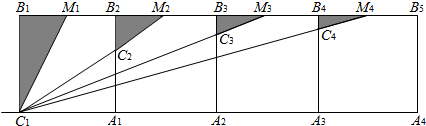
 如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.
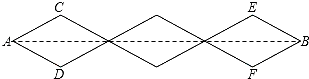
如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m. 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.