题目内容
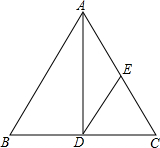 如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是
如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是考点:等腰三角形的判定与性质
专题:
分析:由AD是等腰三角形ABC的底边BC上的高,DE∥AB,易得△EDC是等腰三角形,又由AD⊥BC,易得△AED是等腰三角形.
解答:解:△EDC与△AED.
理由:∵△ABC是等腰三角形,AB=AC,
∴∠B=∠C,
∵DE∥AB,
∴∠EDC=∠B,
∴∠EDC=∠C,
∴ED=EC,
即△EDC是等腰三角形;
∵AD⊥BC,
∴∠EDC+∠ADE=90°,∠C+∠CAD=90°,
∴∠ADE=∠CAD,
∴AE=ED,
∴△AED是等腰三角形.
故答案为:△EDC与△AED.
理由:∵△ABC是等腰三角形,AB=AC,
∴∠B=∠C,
∵DE∥AB,
∴∠EDC=∠B,
∴∠EDC=∠C,
∴ED=EC,
即△EDC是等腰三角形;
∵AD⊥BC,
∴∠EDC+∠ADE=90°,∠C+∠CAD=90°,
∴∠ADE=∠CAD,
∴AE=ED,
∴△AED是等腰三角形.
故答案为:△EDC与△AED.
点评:本题主要考查等腰三角形的判定与性质以及平行线的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
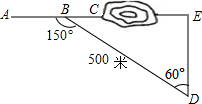 如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=150°,BD=500米,∠D=60°.要使A,C,E成一直线.那么开挖点E离点D的距离是( )
如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=150°,BD=500米,∠D=60°.要使A,C,E成一直线.那么开挖点E离点D的距离是( )| A、200米 | B、250米 |
| C、300米 | D、350米 |
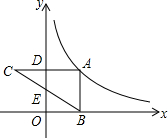 如图,点A在反比例函数y=
如图,点A在反比例函数y=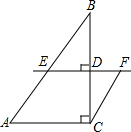 如图,在△ABC中,∠ACB=90°,AC=3,BC=4.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=x.
如图,在△ABC中,∠ACB=90°,AC=3,BC=4.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=x.
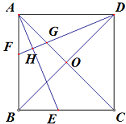 如图所示,四边形ABCD是正方形,AC、BD交于点O,AE平分∠BAC,DF垂直AE,交AB于点F,交AE于点H,交AC于点G.求证:
如图所示,四边形ABCD是正方形,AC、BD交于点O,AE平分∠BAC,DF垂直AE,交AB于点F,交AE于点H,交AC于点G.求证: