题目内容
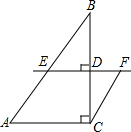 如图,在△ABC中,∠ACB=90°,AC=3,BC=4.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=x.
如图,在△ABC中,∠ACB=90°,AC=3,BC=4.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=x.(1)当x取何值时,四边形EACF是菱形?请说明理由;
(2)当x取何值时,四边形EACD的面积等于3?
考点:菱形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)由题意知四边形EACF为平行四边形,欲使其为菱形,需要CF=AC=3.根据相似三角形△BDE∽△CDF的对应边成比例求得
=
,把相关线段的数据代入可以求得CD的长度;
(2)根据梯形面积公式列出关于x的方程,通过解方程求得x的值.
| BE |
| CF |
| BD |
| CD |
(2)根据梯形面积公式列出关于x的方程,通过解方程求得x的值.
解答:解:(1)由题意知四边形EACF为平行四边形,欲使其为菱形,需要CF=AC=3.
∵∠ACB=90°,AC=2,BC=3,
∴由勾股定理得:AB=5.
又AE=CF=3,故BE=2.
∵CF∥AB,
∴△BDE∽△CDF,
∴
=
,即
=
,
解得 x=
,
即当x=
时四边形EACF为菱形;
(2) ∵DE∥AC,
∵DE∥AC,
∴△BED∽△BAC,
∴
=
,
∴
=
,
解得:DE=3-
x
由S=
(AC+ED)•DC=
×(3-
x+3)x=3,
解得 x1=4+2
(不合题意舍去),x2=4-2
,
所以 x=4-2
时,四边形EACF面积为3.
∵∠ACB=90°,AC=2,BC=3,
∴由勾股定理得:AB=5.
又AE=CF=3,故BE=2.
∵CF∥AB,
∴△BDE∽△CDF,
∴
| BE |
| CF |
| BD |
| CD |
| 4-x |
| x |
| 2 |
| 3 |
解得 x=
| 12 |
| 5 |
即当x=
| 12 |
| 5 |
(2)
 ∵DE∥AC,
∵DE∥AC,∴△BED∽△BAC,
∴
| DE |
| CA |
| BD |
| BC |
∴
| DE |
| 3 |
| 4-x |
| 4 |
解得:DE=3-
| 3 |
| 4 |
由S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
解得 x1=4+2
| 2 |
| 2 |
所以 x=4-2
| 2 |
点评:本题考查了菱形的判定与性质,相似三角形的判定与性质以及勾股定理等知识点.此题利用了菱形的邻边相等的性质.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列运算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、-4
| ||||||||||
D、
|
 用整式填空,如图1(图中长度单位:m),阴影部分的面积
用整式填空,如图1(图中长度单位:m),阴影部分的面积 如图,在菱形ABCD中,DE⊥AB于点E,∠A=60°,BE=4,则梯形BCDE的面积为
如图,在菱形ABCD中,DE⊥AB于点E,∠A=60°,BE=4,则梯形BCDE的面积为 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,E为AB边的中点,EF∥DC,交BC边于点F,若AD=2,BC=6,则EF的长为( )
如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,E为AB边的中点,EF∥DC,交BC边于点F,若AD=2,BC=6,则EF的长为( ) 在如图的4×3网格中,每个小正方形的边长均为1,正方形顶点叫网格格点,连结两个网格格点的线段叫网格线段.
在如图的4×3网格中,每个小正方形的边长均为1,正方形顶点叫网格格点,连结两个网格格点的线段叫网格线段.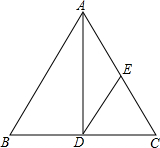 如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是
如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是