题目内容
在一个不透明的盒子里,装有四个分别标有数字1,-2,-3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)小明抽到的数字是负数的概率是 .
(2)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(3)求小明、小华各取一次小球所确定的点(x,y)落在第二象限的概率.
(1)小明抽到的数字是负数的概率是
(2)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(3)求小明、小华各取一次小球所确定的点(x,y)落在第二象限的概率.
考点:列表法与树状图法
专题:
分析:(1)由在一个不透明的盒子里,装有四个分别标有数字1,-2,-3,4的小球,直接利用概率公式求解即可求得答案;
(2)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;
(3)由满足点(x,y)落在第二象限上(记为事件A)的结果有4个,即(-2,1),(-3,1),(-2,4),(-3,4),直接利用概率公式求解即可求得答案.
(2)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;
(3)由满足点(x,y)落在第二象限上(记为事件A)的结果有4个,即(-2,1),(-3,1),(-2,4),(-3,4),直接利用概率公式求解即可求得答案.
解答:解:(1)∵在一个不透明的盒子里,装有四个分别标有数字1,-2,-3,4的小球,
∴小明抽到的数字是负数的概率是:
=
;
故答案为:
.
(2)列表得:
可能出现的结果共有16个,它们出现的可能性相等;
(3)∵满足点(x,y)落在第二象限上(记为事件A)的结果有4个,即(-2,1),(-3,1),(-2,4),(-3,4),
∴P(A)=
=
.
∴小明抽到的数字是负数的概率是:
| 2 |
| 4 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
(2)列表得:
x y |
1 | -2 | -3 | 4 |
| 1 | (1,1) | (-2,1) | (-3,1) | (4,1) |
| -2 | (1,-2) | (-2,-2) | (-3,-2) | (4,-2) |
| -3 | (1,-3) | (-2,-3) | (-3,-3) | (4,-3) |
| 4 | (1,4) | (-2,4) | (-3,4) | (4,4) |
(3)∵满足点(x,y)落在第二象限上(记为事件A)的结果有4个,即(-2,1),(-3,1),(-2,4),(-3,4),
∴P(A)=
| 4 |
| 16 |
| 1 |
| 4 |
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
下列运算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、-4
| ||||||||||
D、
|
 如图,O是矩形ABCD的对角线AC、BD的交点,OM⊥AD,垂足为M,若AB=6,则OM长为
如图,O是矩形ABCD的对角线AC、BD的交点,OM⊥AD,垂足为M,若AB=6,则OM长为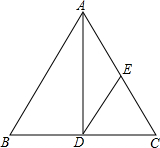 如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是
如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是

 如图,AB是直径,CA切⊙O于点A,连接BC交⊙O点D,E是弧BD的中点,连接AE交BC于点F.
如图,AB是直径,CA切⊙O于点A,连接BC交⊙O点D,E是弧BD的中点,连接AE交BC于点F.