题目内容
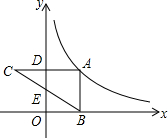 如图,点A在反比例函数y=
如图,点A在反比例函数y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:计算题
分析:连结BD,利用三角形面积公式得到S△ADB=
S△BAC=2,则S矩形OBAD=2S△ADB=4,于是可根据反比例函数的比例系数k的几何意义得到k的值.
| 1 |
| 2 |
解答: 解:连结BD,如图,
解:连结BD,如图,
∵AD=DC,
∴S△ADB=S△BDC=
S△BAC=
×4=2,
∵AD⊥y轴于点D,AB⊥x轴,
∴四边形OBAD为矩形,
∴S矩形OBAD=2S△ADB=2×2=4,
∴k=4.
故答案为:4.
 解:连结BD,如图,
解:连结BD,如图,∵AD=DC,
∴S△ADB=S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD⊥y轴于点D,AB⊥x轴,
∴四边形OBAD为矩形,
∴S矩形OBAD=2S△ADB=2×2=4,
∴k=4.
故答案为:4.
点评:本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
| k |
| x |

练习册系列答案
相关题目
 用整式填空,如图1(图中长度单位:m),阴影部分的面积
用整式填空,如图1(图中长度单位:m),阴影部分的面积 如图,在△ABC中,∠B与∠C的平分线交于点O.过O点作DE∥BC,分别交AB、AC于D、E.若AB=8,AC=6,则△ADE的周长是
如图,在△ABC中,∠B与∠C的平分线交于点O.过O点作DE∥BC,分别交AB、AC于D、E.若AB=8,AC=6,则△ADE的周长是 如图,O是矩形ABCD的对角线AC、BD的交点,OM⊥AD,垂足为M,若AB=6,则OM长为
如图,O是矩形ABCD的对角线AC、BD的交点,OM⊥AD,垂足为M,若AB=6,则OM长为 如图,在菱形ABCD中,DE⊥AB于点E,∠A=60°,BE=4,则梯形BCDE的面积为
如图,在菱形ABCD中,DE⊥AB于点E,∠A=60°,BE=4,则梯形BCDE的面积为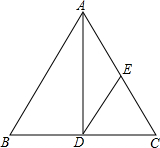 如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是
如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是