题目内容
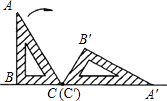 如图,一块含有30°的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C′的位置,若BC=3cm,则:
如图,一块含有30°的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C′的位置,若BC=3cm,则:(1)顶点A从开始到结束共走过的路径有多长?(计算结果保留π)
(2)直角三角形ABC扫过的面积是多少?(计算结果保留π)
考点:弧长的计算,扇形面积的计算,旋转的性质
专题:
分析:(1)根据直角三角形30°角所对的直角边等于斜边的一半可得AC=2BC,再根据直角三角形两锐角互余求出∠ACB=60°,然后求出∠ACA′=120°,最后根据弧长公式即可得出顶点A从开始到结束共走过的路径即为弧的长度;
(2)直角三角形ABC扫过的面积是扇形CAA′的面积与三角形ABC面积的和.
(2)直角三角形ABC扫过的面积是扇形CAA′的面积与三角形ABC面积的和.
解答:解:(1)∵∠A=30°,BC=3cm,
∴AC=2BC=2×3=6cm,
∴AB=3
cm,
∠ACB=90°-∠A=90°-30°=60°,
∴∠ACA′=180°-60°=120°,
顶点A经过的路径长=
=4πcm,
(2)AC旋转到A′C所扫过的扇形面积=
=12πcm2,
S△ABC=
AB•BC=
×3
×3=
cm2,
∴直角三角形ABC扫过的面积=12π+
(cm2).
∴AC=2BC=2×3=6cm,
∴AB=3
| 3 |
∠ACB=90°-∠A=90°-30°=60°,
∴∠ACA′=180°-60°=120°,
顶点A经过的路径长=
| 120•π•6 |
| 180 |
(2)AC旋转到A′C所扫过的扇形面积=
| 120•π•62 |
| 360 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
9
| ||
| 2 |
∴直角三角形ABC扫过的面积=12π+
9
| ||
| 2 |
点评:本题考查了旋转的性质,直角三角形的性质,以及弧长的计算,扇形的面积的计算,熟记各性质并求出AC的长度和∠ACA′=120°是解题的关键.

练习册系列答案
相关题目
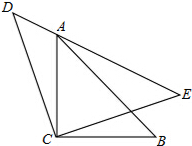 如图,△CAB和△CDE都是等腰直角三角形(C是直角顶点),点A在DE边上,求证:AD2+AE2=2AC2.
如图,△CAB和△CDE都是等腰直角三角形(C是直角顶点),点A在DE边上,求证:AD2+AE2=2AC2. 已知:如图,在△ABC中,BC=2,∠A=45°,∠B=60°,求AC的长.
已知:如图,在△ABC中,BC=2,∠A=45°,∠B=60°,求AC的长.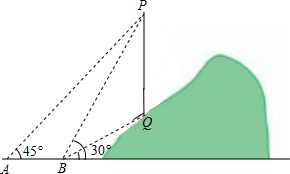 如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.
如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.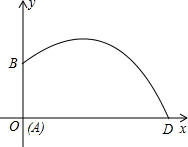 如图,某喷灌设备的喷头B高出地面1.2m,如果喷出的抛物线形水流的水平距离x(m)与高度y(m)之间关系为y=a(x-4)2+2,求水流落地点D与喷头底部A的距离(精确到0.1m)
如图,某喷灌设备的喷头B高出地面1.2m,如果喷出的抛物线形水流的水平距离x(m)与高度y(m)之间关系为y=a(x-4)2+2,求水流落地点D与喷头底部A的距离(精确到0.1m)