题目内容
8.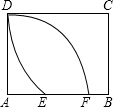 如图所示,以矩形的顶点A为圆心AD的长为半径画圆交AB于点F,再以C为圆心CD的长为半径画圆,交AB于点E,若AD=5,CD=$\frac{17}{3}$,则EF的长是2.
如图所示,以矩形的顶点A为圆心AD的长为半径画圆交AB于点F,再以C为圆心CD的长为半径画圆,交AB于点E,若AD=5,CD=$\frac{17}{3}$,则EF的长是2.
分析 连接CE,可得出CE=CD,由矩形的性质得到BC=AD,在直角三角形BCE中,利用勾股定理求出BE的长,由AB-AF求出BF的长,由BE-BF求出EF的长即可.
解答 解:连接CE,如图所示
根据题意得:CE=CD=$\frac{17}{3}$,BC=AD=5,AF=AD=5,AB=CD=$\frac{17}{3}$,∠B=90°,
∴△BCE为直角三角形,
∴BE=$\sqrt{C{E}^{2}-B{C}^{2}}$=$\frac{8}{3}$,
又∵BF=AB-AF=$\frac{17}{3}$-5=$\frac{2}{3}$,
∴EF=BE-BF=$\frac{8}{3}$-$\frac{2}{3}$=2;
故答案为:2.
点评 此题考查了矩形的性质,以及勾股定理,熟练掌握矩形的性质是解本题的关键.

练习册系列答案
相关题目
19.$\root{3}{27}$的值为( )
| A. | 3 | B. | -3 | C. | -2 | D. | 2 |
17.下列运算正确是( )
| A. | a•a3=a3 | B. | (ab)3=a3b | C. | a8÷a4=a2 | D. | (a3)2=a6 |
 一副三角板按如图所示叠放,其中∠ACB=∠DCE=90°,∠A=30°,∠D=45°,且AC∥DE,则∠BCD=45度.
一副三角板按如图所示叠放,其中∠ACB=∠DCE=90°,∠A=30°,∠D=45°,且AC∥DE,则∠BCD=45度. 如图,在平行四边形ABCD中,AB=6cm,∠BCD的平分线交AD于点E,则线段DE的长度是6 cm.
如图,在平行四边形ABCD中,AB=6cm,∠BCD的平分线交AD于点E,则线段DE的长度是6 cm.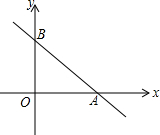 如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B,点M在x轴上,要使△ABM是以AB为腰的等腰三角形,那么点M的坐标是($\sqrt{2}$+1,0)、(-$\sqrt{2}$+1,0)或(-1,0).
如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B,点M在x轴上,要使△ABM是以AB为腰的等腰三角形,那么点M的坐标是($\sqrt{2}$+1,0)、(-$\sqrt{2}$+1,0)或(-1,0).