题目内容
11.操作与证明:把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,点E,F分别在正方形的边CB,AB上,易知:AF=CE,AF⊥CE.(如图1)(不要证明)
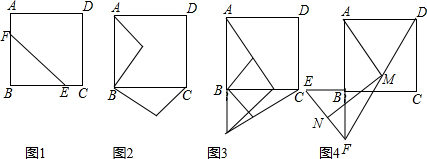
(1)将图1中的直角三角板BEF绕点B顺时针旋转α度(0<α<45),连接AF,CE,(如图2),试证明:AF=CE,AF⊥CE.
猜想与发现:
(2)将图2中的直角三角板BEF绕点B顺时针继续旋转,使BF落在BC边上,连接AF,CE,(如图3),点M,N分别为AF,CE的中点,连接MB,BN.
①MB,BN的数量关系是相等;
②MB,BN的位置关系是垂直.
变式与探究:
(3)图1中的直角三角板BEF绕点B顺时针旋转180°,点M,N分别为DF,EF的中点,连接MA,MN,(如图4),MA,MN的数量关系、位置关系又如何?为什么?
分析 (1)延长AF交EC于G,交BC于H,利用正方形ABCD的性质和等腰△BEF的性质,证明△ABF≌△CBE,得到AF=CE,∠BAF=∠BCE,根据∠BAF+AHB=90°,∠AHB=∠CHG,所以∠BCE+∠CHG=90°,即可解答.
(2)①MB,BN的数量关系是相等;②MB,BN的位置关系是垂直;
(3)MA=MN,MA⊥MN,理由:如图4,连接DE,利用正方形ABCD的性质和等腰△BEF的性质,证明△ADF≌△CDE,得到DF=DE,∠1=∠2,利用在Rt△ADF中,点M是DF的中点,得到MA=$\frac{1}{2}$DF=MD=MF,再利用中位线的性质,得到得到MN=$\frac{1}{2}$DE,MN∥DE,通过角之间的等量代换和三角形内角和,得到∠6=90°,从而得到∠7=∠6=90°,即可解答.
解答 解:(1)如图2,延长AF交EC于G,交BC于H,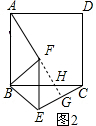
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABF+∠FBC=90°,
∵△BEF是等腰直角三角形,
∴BE=BF,∠EBF=90°,
∴∠CBE+∠FBC=90°,
∴∠ABF=∠CBE,
在△ABF和△CBE中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠CBE}\\{BF=BE}\end{array}\right.$,
∴△ABF≌△CBE,
∴AF=CE,∠BAF=∠BCE,
∵∠BAF+AHB=90°,∠AHB=∠CHG,
∴∠BCE+∠CHG=90°,
∴AF⊥CE.
(2)①相等;②垂直.
故答案为:相等,垂直.
(3)MA=MN,MA⊥MN,
理由:如图4,连接DE,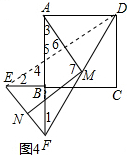
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∵∵△BEF是等腰直角三角形,
∴BE=BF,∠EBF=90°,
∵点E、F分别在正方形CB、AB的延长线上,
∴AB+BF=CB+BE,即AF=CE,
∵$\left\{\begin{array}{l}{AD=CD}\\{∠DAF=∠DCE}\\{AF=DE}\end{array}\right.$,
∴△ADF≌△CDE,
∴DF=DE,∠1=∠2,
在Rt△ADF中,
∵点M是DF的中点,
∴MA=$\frac{1}{2}$DF=MD=MF,
∴∠1=∠3,
∵点N是EF的中点,
∴MN是△DEF的中位线,
∴MN=$\frac{1}{2}$DE,MN∥DE,
∴MA=MN,∠2=∠3,
∵∠2+∠4=∠ABC=90°,∠4=∠5,
∴∠3+∠5=90°,
∴∠6=180°-(∠3+∠5)=90°,
∴∠7=∠6=90°,MA⊥MN.
点评 本题考查了图形的旋转的性质、全等三角形的性质与判定、等腰三角形的性质,解决本题的关键是证明三角形全等,得到相等的边与角,作辅助线也是解决本题的关键.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案| A. | 11×104 | B. | 0.11×107 | C. | 1.1×106 | D. | 1.1×105 |
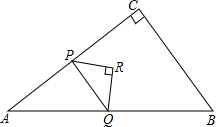 如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).
如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).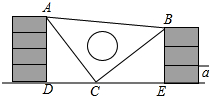 课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,求证:△ADC≌△CEB.
课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,求证:△ADC≌△CEB.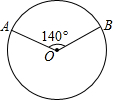 如图,A、B是⊙O上两点,∠AOB=140°,P是⊙O上的一个动点,P不与点A、B重合,则∠APB=70°或110°.
如图,A、B是⊙O上两点,∠AOB=140°,P是⊙O上的一个动点,P不与点A、B重合,则∠APB=70°或110°.