题目内容
3.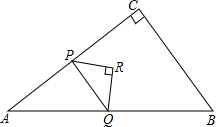 如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).
如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).(1)求点P在AC边上时PQ的长,(用含t的代数式表示);
(2)求点R到AC、PQ所在直线的距离相等时t的取值范围;
(3)当点P在AC边上运动时,求S与t之间的函数关系式;
(4)直接写出点R落在△ABC高线上时t的值.
分析 (1)只需利用三角函数就可解决问题;
(2)可分点P在AC边上(图①)和点P在BC边上(图②)两种情况讨论:当点P在AC边上时,易得点R到AC、PQ所在直线的距离始终相等,从而可得0<t<1;当点P在BC边上时,易得PC=PQ,由此建立关于t的方程,就可解决问题;
(3)可分△PQR全部在△ABC内和△PQR部分在△ABC内两种情况讨论:当△PQR全部在△ABC内时,只需运用三角形的面积公式就可解决问题;当△PQR部分在△ABC内时,只需运用割补法就可解决问题;
(4)可分以下几种情况讨论:点R在AB的高CH上(如图④和图⑦)、点R在AC的高BC上(如图⑤)、点R在BC的高AC上(如图⑥),其中图④和图⑦可通过构造K型全等,并利用相似三角形的性质来解决问题,图5和图6可通过PQ=2PC来解决问题.
解答 解:(1)如图①,
由题意可知AP=4t,
tanA=$\frac{PQ}{AP}$=$\frac{BC}{AC}$=$\frac{3}{4}$,
∴PQ=3t;
(2)①当点P在AC边上时,如图①.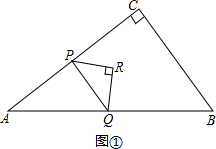
∵∠RPQ=45°,∠CPQ=90°,
∴∠CPR=45°=∠RPQ,
∴点R到直线AC、PQ距离相等,
此时0<t<1.
②当点P在BC边上时,过点R作RH⊥PQ于点H,如图②,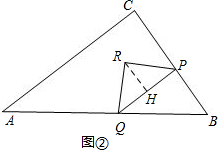
则有PC=4t-4,PB=7-4t,
∵tanB=$\frac{PQ}{PB}$=$\frac{AC}{BC}$=$\frac{4}{3}$,
∴PQ=$\frac{4}{3}$PB=$\frac{4}{3}$(7-4t).
由题可得:RH=$\frac{1}{2}$PC.
∵RH=$\frac{1}{2}$PQ,
∴PC=PQ,
∴4t-4=$\frac{4}{3}$(7-4t),
解得:t=$\frac{10}{7}$.
综上所述:0<t<1或t=$\frac{10}{7}$;
(3)①当0<t≤$\frac{8}{11}$时,如图①.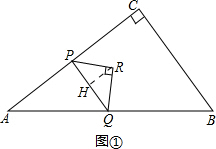
过点R作RH⊥PQ于点H,
S=$\frac{1}{2}$PQ•RH=$\frac{1}{2}$×3t×$\frac{3t}{2}$=$\frac{9}{4}$t2.
②当$\frac{8}{11}$<t<1时,如图③.
过点R作RH⊥PQ于点H,交BC于点G,
则有RG⊥MN,RH=$\frac{1}{2}$PQ=$\frac{3}{2}$t,GH=PC=4-4t,
∴S=S△RPQ-S△RMN=$\frac{1}{2}$PQ•RH-$\frac{1}{2}$MN•RH
=RH2-RG2=($\frac{3}{2}$t)2-[$\frac{3}{2}$t-(4-4t)]2
=-28t2+44t-16;
(4)点R落在△ABC高线上时,t的值为$\frac{32}{53}$,$\frac{8}{11}$,$\frac{13}{10}$,$\frac{67}{46}$.
提示:可分以下几种情况讨论:如图④~⑦
①点P在AC上,且点R在AB的高CH上,如图④,
过点P作PG⊥CH于G,
易证△PGR≌△RHQ,则有PG=RH,GR=QH.
易求得AB=5,CH=$\frac{12}{5}$,AH=$\frac{16}{5}$,BH=$\frac{9}{5}$.
PC=4-4t,CG=$\frac{3}{5}$PC=$\frac{3}{5}$(4-4t),PG=$\frac{4}{5}$PC=$\frac{4}{5}$(4-4t),
AQ=$\frac{5}{4}$AP=5t,QH=AH-AQ=$\frac{16}{5}$-5t.
根据CH=CG+GR+RH=CG+QH+PG=$\frac{12}{5}$,得
$\frac{3}{5}$(4-4t)+$\frac{16}{5}$-5t+$\frac{4}{5}$(4-4t)=$\frac{12}{5}$,
解得:t=$\frac{32}{53}$.
②点P在AC上,且点R在AC的高BC上,如图⑤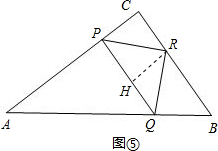
过点R作RH⊥PQ于H,
易得PQ=2RH=2PC,PQ=$\frac{3}{4}$AP=3t,PC=4-4t,
∴3t=2(4-4t),
解得:t=$\frac{8}{11}$.
③点P在BC上,且点R在BC的高AC上,如图⑥,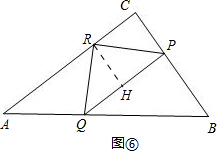
过点R作RH⊥PQ于H,
易得PQ=2RH=2PC,PQ=$\frac{4}{3}$PB=$\frac{4}{3}$(7-4t),PC=4t-4,
∴$\frac{4}{3}$(7-4t)=2(4t-4),
解得:t=$\frac{13}{10}$.
④点P在BC上,且点R在AB的高CH上,如图⑦,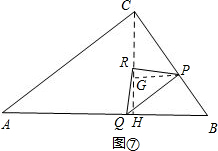
过点P作PG⊥CH于G,
易证△PGR≌△RHQ,则有PG=RH,GR=QH.
易证△CGP∽△CHB,
∴$\frac{CG}{CH}$=$\frac{PG}{BH}$=$\frac{CP}{CB}$.
∵BC=3,CH=$\frac{12}{5}$,BH=$\frac{9}{5}$,CP=4t-4,
∴CG=$\frac{4}{5}$PC=$\frac{4}{5}$(4t-4),PG=$\frac{3}{5}$PC=$\frac{3}{5}$(4t-4),
同理可得QB=$\frac{5}{3}$PB=$\frac{5}{3}$(7-4t),QH=QB-BH=$\frac{5}{3}$(7-4t)-$\frac{9}{5}$.
根据CH=CG+GH=CG+RH-RG=CG+PG-QH=$\frac{12}{5}$,得
$\frac{4}{5}$(4t-4)+$\frac{3}{5}$(4t-4)-[$\frac{5}{3}$(7-4t)-$\frac{9}{5}$]=$\frac{12}{5}$,
解得:t=$\frac{67}{46}$.
点评 本题主要考查了三角函数、等腰直角三角形的性质、直角三角形斜边上的中线等于斜边的一半、角平分线的性质、全等三角形的判定与性质、相似三角形的判定与性质等知识,在解决问题的过程中,用到了割补法和分类讨论等重要的数学思想方法,准确分类是解决本题的关键.

| A. | 5.64×104 | B. | 56.4×104 | C. | 5.64×105 | D. | 0.564×106 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
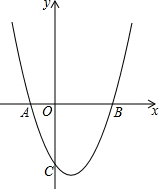 如图,抛物线y=x2-2x+k与x轴交于A,B两点,与y轴交于C(0,-3).
如图,抛物线y=x2-2x+k与x轴交于A,B两点,与y轴交于C(0,-3).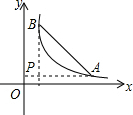 如图,A,B为反比例函数位于第一象限内图象上的点,过点A作x轴的垂线与过点B作y轴垂线交于点P,如果△ABP为等腰直角三角形且A点坐标为(5,1),则△ABP的面积为8.
如图,A,B为反比例函数位于第一象限内图象上的点,过点A作x轴的垂线与过点B作y轴垂线交于点P,如果△ABP为等腰直角三角形且A点坐标为(5,1),则△ABP的面积为8.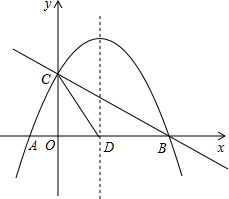 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).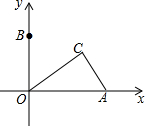 如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.
如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.