题目内容
20.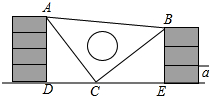 课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,求证:△ADC≌△CEB.
课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,求证:△ADC≌△CEB.
分析 根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可.
解答 证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
∵$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(AAS).
点评 此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
14.下列选项中,显示部分在总体中所占百分比的统计图是( )
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 直方图 |
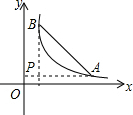 如图,A,B为反比例函数位于第一象限内图象上的点,过点A作x轴的垂线与过点B作y轴垂线交于点P,如果△ABP为等腰直角三角形且A点坐标为(5,1),则△ABP的面积为8.
如图,A,B为反比例函数位于第一象限内图象上的点,过点A作x轴的垂线与过点B作y轴垂线交于点P,如果△ABP为等腰直角三角形且A点坐标为(5,1),则△ABP的面积为8.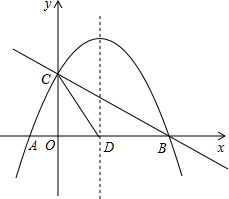 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).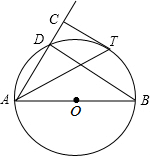 如图,AB是⊙O的直径,D为⊙O上一点,过$\widehat{BD}$上一点T作⊙O的切线TC,且TC⊥AD于点C.
如图,AB是⊙O的直径,D为⊙O上一点,过$\widehat{BD}$上一点T作⊙O的切线TC,且TC⊥AD于点C.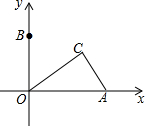 如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.
如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.