题目内容
9．
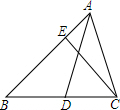如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=50°，则∠ADC的度数为70°．
分析 根据角平分线的定义求出∠DAC，根据直角三角形两锐角互余求出∠ACE，再求出∠ACD，然后利用三角形的内角和即可得解．
解答 解：∵AD是△ABC的角平分线，∠BAC=60°，
∴∠DAC=30°，
∵CE是△ABC的高，
∴∠AEC=90°，
∴∠ACE=30°，
∴∠ACD=80°，
在△ACD中，∠ADC=180°-30°-80°=70°，
故答案为：70°．
点评 本题考查了三角形的内角和定理，角平分线的定义，熟记概念并准确识图，理清图中各角度之间的关系是解题的关键．
练习册系列答案
相关题目
如图，数轴上点A所对应的数是-$\sqrt{5}$．
17．
如图，AD平分∠BAC，DE⊥AB于点E，S△ACD=3，DE=2，则AC长是（ ）
如图，AD平分∠BAC，DE⊥AB于点E，S△ACD=3，DE=2，则AC长是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
4．下列各式中，计算不正确的是（ ）
| A． | （$\sqrt{3}$）2=3 | B． | $\sqrt{（-3）^{2}}$=-3 | C． | （a5）2=a10 | D． | 2a2•（-3a3）=-6a5 |
一个正方体六个面分别标有字母A、B、C、D、E、F，其展开如图所示，已知：A=x2-2xy、B=A-C，C=3xy+y2，若该正方体相对两个面上的多项式的和相等，试用x、y的代数式表示多项式D，并求当x=-1，y=-2时，多项式D的值．
如图是抛物线y1=ax2+bx+c（a≠0）的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：