题目内容
6. 如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.
如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.(1)求证:四边形HDGE是平行四边形.
(2)已知∠C=90°,∠A=30°,AB=4.
①当AG为何值时,四边形HDGE是矩形;
②当AG为何值时,四边形HDGE是菱形.
分析 (1)由平行四边形的判定直接推出;
(2)根据直角三角形的性质得到AB=4,求得AC=2$\sqrt{3}$,BC=4×$\frac{1}{2}$=2,∠B=60°,根据三角形的中位线得到BE=1,DE=2,AD=$\sqrt{3}$,DF=EF=1,根据平行线的性质得到∠CBD=∠B=60°,①当AG=3或2时,四边形HDGE是矩形.当AG=3时,根据全等三角形的性质得到∠DGE=∠DCE=90°,于是得到四边形HDGE是矩形;
当AG=2时,则AG=BG,推出∠DCE=90°,于是得到四边形HDGE是矩形;②过F作MN⊥DE,交AC于M,AB与N,根据全等三角形的性质得到∠MDF=∠A=30°根据线段垂直平分线的性质得到ND=NE,求得AN=AM•com∠A=$\frac{5}{2}$,当AG=AN=$\frac{5}{2}$时,G在DE的中垂线上,根据菱形的判定即可得到结论.
解答  (1)证明:∵HF=GF,DF=EF,
(1)证明:∵HF=GF,DF=EF,
∴四边形HDGE是平行四边形;
(2)解:∵∠C=90°,∠A=30°,AB=4,
∴AC=AB•com∠A=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,BC=4×$\frac{1}{2}$=2,∠B=60°,
∵AC的中点为D,BC的中点为E,F是DE的中点,
∴BE=1,DE=$\frac{1}{2}$AB=2,AD=CD=$\sqrt{3}$,DF=EF=1,DE∥AB,
∴∠CBD=∠B=60°,
①当AG=3或2时,四边形HDGE是矩形,
当AG=3时,如图1,BG=4-3=1,
∴BG=CE,
BG=BE=EG=1=CE,DE=DE,∠CED=∠DEG=60°,
在△DGE和△DCE中,$\left\{\begin{array}{l}{CE=GE}\\{∠CED=∠DEG}\\{DE=DE}\end{array}\right.$,
∴△DGE≌△DCE,
∴∠DGE=∠DCE=90°,
∴四边形HDGE是矩形;
当AG=2时,则AG=BG,
∴DG∥CE,EG∥AC,H,C重合,
∴∠DCE=90°,∴四边形HDGE是矩形,如图2;
②过F作MN⊥DE,交AC于M,AB与N,
∵DE∥AB,
∴MN⊥AB,∠MDF=∠A=30°,
∵F是DE的中点,
∴MN是线段DE的垂直平分线,
∴ND=NE,
∵DF=1,MB=$\frac{2\sqrt{3}}{3}$,
∵AD=$\sqrt{3}$,
∴AM=$\frac{5\sqrt{3}}{3}$,
∴AN=AM•com∠A=$\frac{5\sqrt{3}}{3}$•$\frac{\sqrt{3}}{2}$=$\frac{5}{2}$,
当AG=AN=$\frac{5}{2}$时,G在DE的中垂线上,DG=GE,四边形HDGE是菱形.
点评 本题主要考查了平行四边形的判定和性质,矩形,菱形的判定,平行线的性质,等边三角形的判定和性质,线段垂直平分线的判定和性质,全等三角形的判定与性质,三角函数的定义,综合性强,要注意分类思想的应用,熟练掌握矩形,菱形的判定方法是解题的关键.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案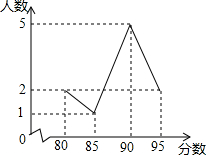 在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )| A. | 95 | B. | 90 | C. | 85 | D. | 80 |
 如图,AB是⊙O的直径,点C,D都在⊙O上,连结CA,CB,DC,DB.已知∠D=30°,BC=3,则AB的长是( )
如图,AB是⊙O的直径,点C,D都在⊙O上,连结CA,CB,DC,DB.已知∠D=30°,BC=3,则AB的长是( )| A. | 5 | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 6 |
| A. | $\left\{\begin{array}{l}{x+y=20}\\{2x+y=12}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{x+2y=20}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=12}\\{2x+y=20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=12}\\{x+2y=20}\end{array}\right.$ |
| A. | 10x+6=12x-6 | B. | 10x-6=12x+6 | C. | $\frac{x-6}{10}=\frac{x+6}{12}$ | D. | $\frac{x+6}{10}=\frac{x-6}{12}$ |
| A. | 64×104 | B. | 6.4×105 | C. | 6.4×104 | D. | 0.64×105 |
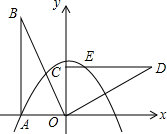 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴上,顶点B的坐标为(-2,4),抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A,将Rt△OAB绕着点O按顺时针方向旋转90°得到△OCD,点C为点A的对应点,点E为抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c于线段CD的交点.
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴上,顶点B的坐标为(-2,4),抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A,将Rt△OAB绕着点O按顺时针方向旋转90°得到△OCD,点C为点A的对应点,点E为抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c于线段CD的交点.