题目内容
1. 已知二次函数y=4x2-4ax+a2-2a+2,
已知二次函数y=4x2-4ax+a2-2a+2,(1)当a=0,2,4时,请在同一直角坐标系中画出对应函数图象的顶点,并画出a=2 时的函数图象;
(2)证明当a取任意实数时,顶点在一条确定的直线上;
(3)求(2)中的直线被抛物线y=4x2-4ax+a2-2a+2截得的线段长.
分析 (1)利用配方法将二次函数解析式由一般式变形为顶点式,由此可得出抛物线的顶点坐标,分别代入a=0、a=2、a=4找出顶点坐标,并画出a=2时,二次函数的图象即可;
(2)由抛物线的顶点坐标为($\frac{1}{2}$a,-2a+2),消去a后即可得出y=-4x+2,此题得证;
(3)联立两函数解析式成方程组,通过解方程组求出交点坐标,再根据两点间的距离公式求出线段长度即可.
解答 解:(1)∵二次函数y=4x2-4ax+a2-2a+2=4(x-$\frac{1}{2}$a)2-2a+2,
∴抛物线的顶点坐标为($\frac{1}{2}$a,-2a+2).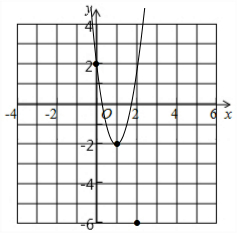
当a=0时,抛物线的顶点坐标为(0,2);
当a=2时,抛物线的顶点坐标为(1,-2),抛物线的解析式为y=4(x-1)2-2;
当a=4时,抛物线的顶点坐标为(2,-6).
画出函数图象如图所示.
(2)证明:∵抛物线的顶点坐标为($\frac{1}{2}$a,-2a+2),
∴-2a+2=-4×($\frac{1}{2}$a)+2,
∴y=-4x+2,即当a取任意实数时,顶点在一条确定的直线上.
(3)联立两函数解析式成方程组,
$\left\{\begin{array}{l}{y=-4x+2}\\{y=4{x}^{2}-4ax+{a}^{2}-2a+2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=\frac{1}{2}a-1}\\{{y}_{1}=-2a+6}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{1}{2}a}\\{{y}_{2}=-2a+2}\end{array}\right.$,
∴两函数的交点坐标为($\frac{1}{2}$a-1,-2a+6),($\frac{1}{2}$a,-2a+2),
∴(2)中的直线被抛物线y=4x2-4ax+a2-2a+2截得的线段长为$\sqrt{[\frac{1}{2}a-(\frac{1}{2}a-1)]^{2}+[-2a+2-(-2a+6)]^{2}}$=$\sqrt{17}$.
点评 本题考查了二次函数的三种形式、二次函数的性质、二次函数的图象以及两点间的距离公式,解题的关键是:(1)利用配方法将二次函数解析式由一般式变形为顶点式;(2)消去a找出顶点坐标所在的直线;(3)联立两函数解析式成方程组,通过解方程组求出两函数图象的交点坐标.

| A. | a=1.5,b=3,c=3 | B. | a=7,b=24,c=25 | C. | a=6,b=8,c=10 | D. | a=3,b=4,c=5 |
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
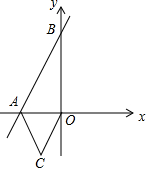 如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )
如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 4-$\sqrt{3}$ | D. | 4$+\sqrt{3}$ |
| A. | 正方形 | B. | 正六边形 | C. | 正八边形 | D. | 正三角形 |
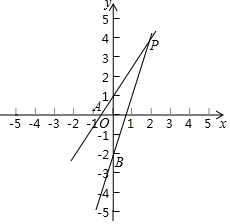 已知直线y=$\frac{5}{2}$x+1与y=5x-2的交点为P,两直线分别交y轴于A、B,求△PAB的面积(画图说明).
已知直线y=$\frac{5}{2}$x+1与y=5x-2的交点为P,两直线分别交y轴于A、B,求△PAB的面积(画图说明). 如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的左视图是( )
如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的左视图是( )



 已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.