题目内容
9.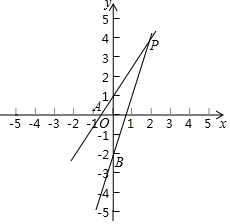 已知直线y=$\frac{5}{2}$x+1与y=5x-2的交点为P,两直线分别交y轴于A、B,求△PAB的面积(画图说明).
已知直线y=$\frac{5}{2}$x+1与y=5x-2的交点为P,两直线分别交y轴于A、B,求△PAB的面积(画图说明).
分析 过点P作PC⊥y轴于点C,利用两直线的解析式分别求出P、A、B的坐标后,即可得出AB与PC的长度,从而可求出△PAB的面积.
解答 解:联立$\left\{\begin{array}{l}{y=\frac{5}{2}x+1}\\{y=5x-2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=\frac{6}{5}}\\{y=4}\end{array}\right.$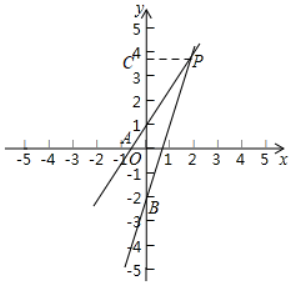
∴P($\frac{6}{5}$,4)
过点P作PC⊥y轴于点C,
∴PC=$\frac{6}{5}$
令x=0分别代入y=$\frac{5}{2}$x+1与y=5x-2,
∴A(0,1),B(0,-2),
∴AB=3,
∴S△PAB的面积为:$\frac{1}{2}$PC•AB=$\frac{1}{2}$×$\frac{6}{5}$×3=$\frac{9}{5}$
点评 本题考查一次函数的综合问题,涉及联立解析式求交点坐标,三角形面积公式,解方程等知识,本题属于中等题型.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
20.以下式子中,一定是二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{3x}$ | C. | $\root{3}{9}$ | D. | $\sqrt{2x+1}$ |
18.若关于x的分式方程$\frac{x}{x-5}$=3-$\frac{m}{5-x}$有增根,则m的值为 ( )
| A. | -5 | B. | 5 | C. | 2 | D. | 不存在 |
19.已知实数a,b,c满足a+b+c=0且a<b<c.则一次函数y=($\frac{c}{a}$+2)x+$\frac{b}{c}$的图象一定经过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、三、四象限 | D. | 第一、二、三象限 |
 已知二次函数y=4x2-4ax+a2-2a+2,
已知二次函数y=4x2-4ax+a2-2a+2,