题目内容
5.①$\frac{()}{3x}$=$\frac{5x{y}^{2}}{3{x}^{2}y}$②$\frac{x-1}{x-2}$=$\frac{1-x}{()}$.
分析 根据分式的分子分母都乘以(或除以)同一个不为零整式,分式的值不变,可得答案.
解答 解:①$\frac{5y}{3x}$=$\frac{5x{y}^{2}}{3{x}^{2}y}$,
②$\frac{x-1}{x-2}$=$\frac{1-x}{2-x}$,
故答案为:5y,2-x.
点评 此题考查了分式的基本性质,关键是熟悉分式的分子分母都乘以(或除以)同一个不为零整式,分式的值不变的知识点.

练习册系列答案
相关题目
15.(-2)3表示( )
| A. | -2×3 | B. | (-2)+(-2)+(-2) | C. | -2×2×2 | D. | (-2)×(-2)×(-2) |
14.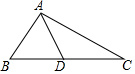 如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )
如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )
 如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )
如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |