题目内容
3.(1)计算:$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{12}$(2)解方程组:$\left\{\begin{array}{l}2x+3y=16\\ x+4y=13\end{array}\right.$.
分析 (1)根据二次根式的加减法则,求出$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{12}$的值是多少即可.
(2)根据解二元一次方程组的方法,求出$\left\{\begin{array}{l}2x+3y=16\\ x+4y=13\end{array}\right.$的解是多少即可.
解答 解:(1)$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{12}$
=3$\sqrt{3}$-$\frac{1}{3}$×3$\sqrt{2}$-2$\sqrt{3}$
=$\sqrt{3}$-$\sqrt{2}$
(2)$\left\{\begin{array}{l}{2x+3y=16(1)}\\{x+4y=13(2)}\end{array}\right.$
由(2),可得x=13-4y(3),
把(3)代入(1),可得
2(13-4y)+3y=16,
整理,可得
-5y+26=16,
解得y=2,
∴x=13-4y
=13-4×2
=13-8
=5
∴原方程组的解是$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$.
点评 此题主要考查了二次根式的加减法,以及解二元一次方程组的方法,要熟练掌握,解答此题的关键是要明确:二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.

练习册系列答案
相关题目
14.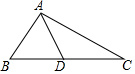 如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )
如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )
 如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )
如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
11.要调查下面的问题,其中最适合普查的是( )
| A. | 调查某种计算机的使用寿命 | B. | 调查CCTV某档电视节目的收视情况 | ||
| C. | 调查我国七年级学生的视力情况 | D. | 调查你所在的班级学生的视力情况 |
18.下列各式的计算,结果正确的是( )
| A. | 3a+2b=5ab | B. | m2-n2=0 | C. | 5x+2x=7x2 | D. | 5xy-5yx=0 |
8.一个口袋中有2个红球,3个白球,这些球除色外都相同,从口袋中随机摸出一个球,这个球是白球的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
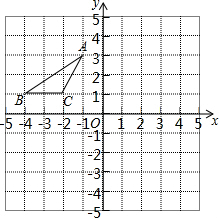 如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC向右平移5个单位,向上平移1个单位得△A1B1C1,再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC向右平移5个单位,向上平移1个单位得△A1B1C1,再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.