题目内容
2.⊙O半径为5,圆心O的坐标为(0,0),点P的坐标为(3,4),则点P在⊙O上(填“内”“上”“外”).分析 先利用两点间的距离公式计算出OA,然后根据点与圆的位置关系的判定方法判断点A与⊙O的位置关系.
解答 解:∵点A的坐标为(3,4),
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴点A到圆心的距离等于圆的半径,
∴点A在⊙O上.
故答案为:上.
点评 本题考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外?d>r;点P在圆上?d=r;点P在圆内?d<r.点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.

练习册系列答案
相关题目
14. 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )
 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )| A. | 50°和30° | B. | 40°和70° | C. | 30°和 20° | D. | 20°和70° |

 如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.若CF=6.BD=2,求AB的长.
如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.若CF=6.BD=2,求AB的长.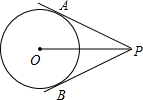 如图,P是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA=4cm,PC=2cm,求∠APB的大小.
如图,P是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA=4cm,PC=2cm,求∠APB的大小.