题目内容
8.同一平面上有2个点,可以画1条直线(如图1);同一平面上有3个点,且不共线,可以画3条直线(如图2);同一平面上有4个点,且任意三点不共线,可以画6条直线(如图3);…,同一平面上有n个点,且任意三点不共线,这n个点可画直线的条数为an.(1)当n=5时,an=10;当n=7时,an=21;
(2)用含有n的代数式表示an,则an=$\frac{n(n-1)}{2}$.
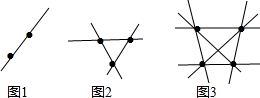
分析 根据过两点的直线有1条,过不在同一直线上的三点的直线有3条,过任何三点都不在一条直线上四点的直线有6条,按此规律,由特殊到一般,总结出公式:平面内任意三个点都不在同一直线上,平面内有n个点,一共可以画直线的条数为$\frac{n(n-1)}{2}$,由此进一步计算即可.
解答 解:(1)平面内有三个点,一共可以画2+1=3条直线;
平面内有四个点,一共可以画3+2+1=4×3÷2=6条直线;
平面内有五个点,一共可以画4+3+2+1=5×4÷2=10条直线;
因此当n=5时,an=10;当n=7时,an=21;
(2)平面内有n个点,则an=(n-1)+…+4+3+2+1=$\frac{n(n-1)}{2}$条直线.
故答案为:10,7,$\frac{n(n-1)}{2}$.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
18.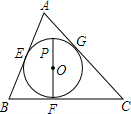 如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )
如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )
 如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )
如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
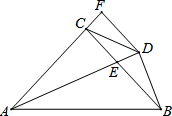 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论: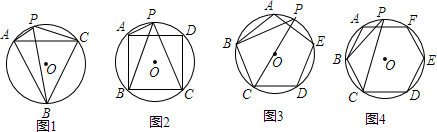
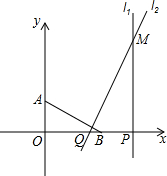 如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒
如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒