题目内容
设a,b是整数,方程x2+ax+b=0的根是
,则a+b= .
4-2
|
考点:一元二次方程的解
专题:
分析:方程的一个根x=
=
-1,代入方程,由a,b是整数,列出关于a,b的方程组,求出a+b的值.
4-2
|
| 3 |
解答:解:把x=
=
=
=
-1代入方程有:
4-2
+(
-1)a+b=0,
4-a+b+(a-2)
=0,
∴
,
∴
,
∴a+b=0.
故答案为0.
4-2
|
3-2
|
(
|
| 3 |
4-2
| 3 |
| 3 |
4-a+b+(a-2)
| 3 |
∴
|
∴
|
∴a+b=0.
故答案为0.
点评:本题考查的是一元二次方程的解,把方程的解代入方程,根据二次根式的性质化简,得到关于a,b的方程组,求出a,b的值,即可求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
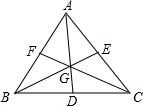 已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证:
已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证: 如图,在△ABC中,BC=4,AC=2
如图,在△ABC中,BC=4,AC=2 如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.