题目内容
已知关于y的方程
=
+
（f1≠f2），则y= ．
| 1 |
| f1 |
| 1 |
| f2 |
| 1 |
| y |
考点：分式的加减法
专题：
分析：先去分母，把分式方程化为整式方程，再解关于y的一元一次方程，从而得出答案．
解答：解：方程两边同乘以f1f2y，得
f2y=f1y+f1f2，
移项得，f2y-f1y=f1f2，
合并同类项得（f2-f1）y=f1f2，
∵f1≠f2，
∴系数化为1，得y=
，
故答案为
．
f2y=f1y+f1f2，
移项得，f2y-f1y=f1f2，
合并同类项得（f2-f1）y=f1f2，
∵f1≠f2，
∴系数化为1，得y=
| f1f2 |
| f2-f1 |
故答案为
| f1f2 |
| f2-f1 |
点评：本题考查了分式的加减，以及分式方程的解法，是基础知识要熟练掌握．
练习册系列答案
相关题目
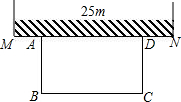如图，某农场老板准备建造一个矩形羊圈ABCD，他打算让矩形羊圈的一面完全靠着墙MN，墙MN可利用的长度为25m，另外三面用长度为50m的篱笆围成（篱笆正好要全部用完，且不考虑接头的部分）
如图，一艘海上巡逻船在A巡航，这时接到B海上指挥中心紧急通知：在指挥中心北偏西60°方向的C有一艘渔船遇险，要求马上前去救援．此时C位于A北偏西30°方向上，A位于B北偏西75°方向上．AB之间的距离为12．求A、C两地之间的距离．（参考数据：
如图，在⊙O中，弦AC与BD交于E，AB=8，AE=6，ED=3，则CD等于