题目内容
 如图,在△ABC中,BC=4,AC=2
如图,在△ABC中,BC=4,AC=2| 3 |
考点:勾股定理,二次函数的最值
专题:
分析:首先根据在△ABC中,已知BC=4,AC=2
,∠ABC=60°,设AD=x,列出△APD的面积关于x的二次函数,利用配方法求得最大值,即为所求△APD的面积最大值.
| 3 |
解答: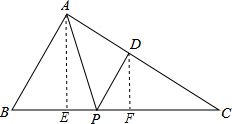 解:过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
解:过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
∵在△ABC中,BC=4,AC=2
,∠ABC=60°,
∴△ABC为Rt△,∠C=30°,
设AD=x,
∵BC=4,∠C=30°,
∴CE=AC•sin∠C=2
×
=3,
∴CD=2
-x,
∴AE=AC•sin30°=
,DF=CD•sin30°=
(2
-x),
∵AB∥PD,
∴PC:BC=CD:AC,
∴PC=3-
x,
∴S△PAD=S△PAC-S△PCD=
×(3-
x)×
-
×(3-
x)×
(2
-x)=-
(x-
)2+
.
∴当PC=3-
x=
时,最大值为
.
 解:过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
解:过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.∵在△ABC中,BC=4,AC=2
| 3 |
∴△ABC为Rt△,∠C=30°,
设AD=x,
∵BC=4,∠C=30°,
∴CE=AC•sin∠C=2
| 3 |
| ||
| 2 |
∴CD=2
| 3 |
∴AE=AC•sin30°=
| 3 |
| 1 |
| 2 |
| 3 |
∵AB∥PD,
∴PC:BC=CD:AC,
∴PC=3-
| ||
| 2 |
∴S△PAD=S△PAC-S△PCD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 8 |
| ||
| 2 |
3
| ||
| 32 |
∴当PC=3-
| ||
| 2 |
| 9 |
| 4 |
3
| ||
| 32 |
点评:本题考查三角形面积的计算、三角函数、直角三角形的性质.解决本题的关键点是证得△ABC为Rt△,从而利用三角函数建立起边间的关系;并在解题过程中转化成求二次函数的最值问题.

练习册系列答案
相关题目
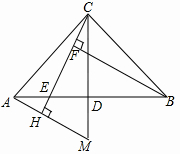 已知,如图所示,在△ABC中,AC=BC,∠ACB=90°,CD平分∠ACB交AB于D,点E是AB边上一点.直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M,找出图中与BE相等的线段,并证明.
已知,如图所示,在△ABC中,AC=BC,∠ACB=90°,CD平分∠ACB交AB于D,点E是AB边上一点.直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M,找出图中与BE相等的线段,并证明.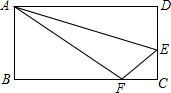 如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.
如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.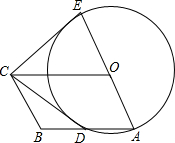 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线, 如图,在⊙O中,弦AC与BD交于E,AB=8,AE=6,ED=3,则CD等于
如图,在⊙O中,弦AC与BD交于E,AB=8,AE=6,ED=3,则CD等于