题目内容
17.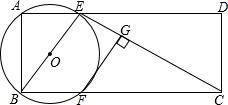 如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.
如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.(1)当点F是BC的中点时,求证:直线FG与⊙O相切;
(2)若FG∥BE时,求AE的长.
分析 (1)连接OF,由点F是BC的中点,得到BF=CF,在矩形ABCD中,∠A=90°,证得BE是⊙O的直径,求得BO=OE,根据三角形的中位线的性质得到OF∥CE,证得OF⊥FG,即可得到结论;
(2)根据平行线的性质得到BE⊥CE,由余角的性质得到∠ABE=∠DEC,证得△ABE∽△CDE,根据相似三角形的性质即可得到结论.
解答 (1)证明:连接OF, ∵点F是BC的中点,
∵点F是BC的中点,
∴BF=CF,
在矩形ABCD中,∵∠A=90°,
∴BE是⊙O的直径,
∴BO=OE,
∴OF∥CE,
∵FG⊥CE,
∴OF⊥FG,
∴直线FG与⊙O相切;
(2)解:∵FG∥BE,FG⊥CE,
∴BE⊥CE,
∴∠AEB+∠DEC=90°,
∵∠ABE+∠AEB=90°,
∴∠ABE=∠DEC,
∵∠A=∠D=90°,
∴△ABE∽△CDE,
∴$\frac{AB}{DE}=\frac{AE}{CD}$,
∵AB=2,AD=5,
∴CD=AB=2,
∴$\frac{2}{5-AE}=\frac{AE}{2}$,
∴AE=1,或AE=4.
点评 本题考查的是切线的判定,三角形的中位线的性质,相似三角形的判定和性质,平行线的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5.56.2万平方米用科学记数法表示正确的是( )
| A. | 5.62×104m2 | B. | 56.2×104m2 | C. | 5.62×105m2 | D. | 0.562×103m2 |
6.某天蔬菜经营户用120元批发了西兰花和胡萝卜共60kg到菜市场零售,西兰花和胡萝卜当天的批发价和零售价如表所示:
如果他当天全部卖完这些西兰花和胡萝卜可获得利润多少元.
| 品名 | 西兰花 | 胡萝卜 |
| 批发价(元/kg) | 2.8 | 1.6 |
| 零售价(元/kg) | 3.8 | 2.5 |
 如图,在平面直角坐标系xOy中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BE=4EC,且△ODE的面积是5,则k的值为$\frac{25}{12}$.
如图,在平面直角坐标系xOy中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BE=4EC,且△ODE的面积是5,则k的值为$\frac{25}{12}$.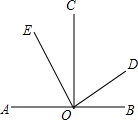 如图,CO⊥AB,垂足为O,∠COE-∠BOD=4°,∠AOE+∠COD=116°,则∠AOD=150°.
如图,CO⊥AB,垂足为O,∠COE-∠BOD=4°,∠AOE+∠COD=116°,则∠AOD=150°.