Question

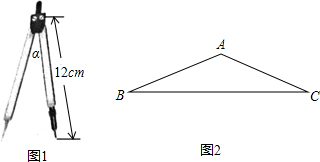如图1，圆规两脚形成的角α称为圆规的张角．一个圆规两脚均为12cm，最大张角150°，你能否画出一个半径为20cm的圆？请借助图2说明理由．（参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

Answer 1

考点：解直角三角形的应用

专题：

分析：先根据等腰三角形的性质求出∠B的度数，过点A作AD⊥BC于点D，根据锐角三角函数的定义可求出BD的长，故可得出结论．

解答：解：∵△ABC是等腰三角形，∠A=150°，
∴∠B=∠C=

180°-150°

2

=15°，
过点A作AD⊥BC于点D，
∴BD=AB•cos∠B≈12×0.97≈11.6cm＜20cm，
∴不能画出一个半径为20cm的圆．

点评：本题考查的是解直角三角形的应用，熟知锐角三角函数的定义是解答此题的关键．