题目内容
2.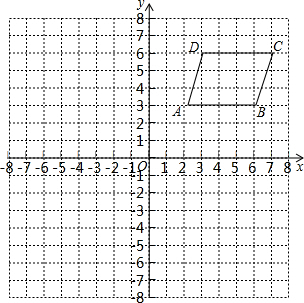 如图,建立平面直角坐标系,点A、B、C、D都在方格的格点上,
如图,建立平面直角坐标系,点A、B、C、D都在方格的格点上,①分别写出A、B、C、D的坐标;
②把四边形ABCD平移,使点C平移到点(-2,4)处,画出平移后的四边形;
③求平行四边形ABCD的面积.
分析 ①根据直角坐标系的特点分别写出A、B、C、D的坐标;
②将点C平移到点(-2,4)处,即将四边形ABCD先向左平移9个单位,再向下平移2个单位,据此作出平移后的四边形;
③平行四边形的面积=底×高,据此求出面积.
解答 解:①A(2,3),B(6,3),C(7,6),D(3,6);
②所作图形如图所示:
③S?ABCD=4×3=12.
点评 本题考查了根据平移变换作图,解答本题的关键是根据网格结构和直角坐标系的特点作出各点的位置,然后顺次连接.

练习册系列答案
相关题目
17.一个三角形的三个内角之比是2:3:4,则此三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 以上三种都有可能 |
7.下列计算正确的是( )
| A. | $\sqrt{4}$-$\sqrt{3}$=1 | B. | $\sqrt{6}$÷$\sqrt{3}$=2 | C. | -2$\sqrt{3}$=$\sqrt{(-2)^{2}×3}$ | D. | $\sqrt{2}$×$\sqrt{\frac{1}{2}}$=1 |