题目内容
12.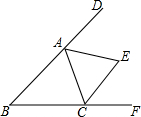 如图,在△ABC中,三角形的外角∠DAC和∠ACF的平分线交于点E,若∠AEC=70°,则∠B=40°.
如图,在△ABC中,三角形的外角∠DAC和∠ACF的平分线交于点E,若∠AEC=70°,则∠B=40°.
分析 先根据三角形内角和定理求出∠EAC+∠ACE的度数,再根据AE、CE分别是∠DAC与∠ACF的角平分线得出∠DAC+∠ACF的度数,进而得出∠BAC+∠ACB的度数,根据三角形内角和定理即可得出结论
解答 解:∵△ACE中,∠AEC=70°,
∴∠EAC+∠ACE=180°-70°=110°,
∵AE、CE分别是∠DAC与∠ACF的角平分线,
∴∠DAC+∠ACF=2(∠EAC+∠ACE)=220°,
∴∠BAC+∠ACB=360°-220°=140°,
∴∠B=180°-140°=40°.
故答案为:40°.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
3.已知a-b=3,b+c=-4,则代数式ac-bc+a2-ab的值为( )
| A. | 4 | B. | -4 | C. | 3 | D. | -3 |
7.计算$\sqrt{12}×\sqrt{\frac{1}{3}}+\sqrt{8}$的结果是( )
| A. | 6$+2\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 2$+2\sqrt{2}$ |
17.以下列各组数为边长,能组成直角三角形的是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 6,8,10 | C. | 5,12,17 | D. | 9,40,42 |
 如图,是每一个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“大”相对的面上的汉字是堰.
如图,是每一个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“大”相对的面上的汉字是堰.