题目内容
4.(1)计算:$\sqrt{\frac{1}{7}}+\sqrt{28}-\sqrt{700}$(2)解下列方程组:$\left\{\begin{array}{l}{3x+4y=10}\\{4x+y-9=0}\end{array}\right.$.
分析 (1)首先化简二次根式,进而合并同类二次根式即可;
(2)利用代入消元法解方程组得出答案.
解答 解:(1)$\sqrt{\frac{1}{7}}+\sqrt{28}-\sqrt{700}$
=$\frac{\sqrt{7}}{7}$+2$\sqrt{7}$-10$\sqrt{7}$
=-$\frac{55\sqrt{7}}{7}$;
(2)$\left\{\begin{array}{l}{3x+4y=10}\\{4x+y-9=0}\end{array}\right.$
整理得:
$\left\{\begin{array}{l}{3x+4y=10①}\\{4x+y=9②}\end{array}\right.$,
由②得,y=9-4x,代入3x+4y=10,
故3x+4(9-4x)=10,
解得:x=2,
故y=1,
故方程组的解集为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 此题主要考查了二次根式的加减以及二元一次方程组的解法,正确化简二次根式是解题关键.

练习册系列答案
相关题目
14. 如图,一块直角三角板ABC,∠B=90°,AB=3,BC=4,截得两个正方形,DEFG、BDEF,设S1=DEFG的面积,S2=BDEF的面积,则S1、S2的大小关系是( )
如图,一块直角三角板ABC,∠B=90°,AB=3,BC=4,截得两个正方形,DEFG、BDEF,设S1=DEFG的面积,S2=BDEF的面积,则S1、S2的大小关系是( )
 如图,一块直角三角板ABC,∠B=90°,AB=3,BC=4,截得两个正方形,DEFG、BDEF,设S1=DEFG的面积,S2=BDEF的面积,则S1、S2的大小关系是( )
如图,一块直角三角板ABC,∠B=90°,AB=3,BC=4,截得两个正方形,DEFG、BDEF,设S1=DEFG的面积,S2=BDEF的面积,则S1、S2的大小关系是( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 无法确定 |
15. 如图是某月的日历,在此日历上用一个正方形圈出9个数(如6、7、8、13、14、15、20、21、22).若圈出的9个数中,最大数与最小数的和为32,则这9个数的和为( )
如图是某月的日历,在此日历上用一个正方形圈出9个数(如6、7、8、13、14、15、20、21、22).若圈出的9个数中,最大数与最小数的和为32,则这9个数的和为( )
 如图是某月的日历,在此日历上用一个正方形圈出9个数(如6、7、8、13、14、15、20、21、22).若圈出的9个数中,最大数与最小数的和为32,则这9个数的和为( )
如图是某月的日历,在此日历上用一个正方形圈出9个数(如6、7、8、13、14、15、20、21、22).若圈出的9个数中,最大数与最小数的和为32,则这9个数的和为( )| A. | 144 | B. | 153 | C. | 198 | D. | 216 |
19.点A(x1,y1),点B(x2,y2)是一次函数y=-2x-4图象上的两点,且x1<x2,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1>y2>0 | C. | y1<y2 | D. | y1=y2 |
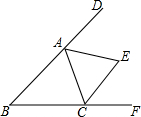 如图,在△ABC中,三角形的外角∠DAC和∠ACF的平分线交于点E,若∠AEC=70°,则∠B=40°.
如图,在△ABC中,三角形的外角∠DAC和∠ACF的平分线交于点E,若∠AEC=70°,则∠B=40°.
 小明在元旦为好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“祝你学年快乐”,其中“祝”的对面是“新”,“快”的对面是“乐”,则它的平面展开图可能是( )
小明在元旦为好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“祝你学年快乐”,其中“祝”的对面是“新”,“快”的对面是“乐”,则它的平面展开图可能是( )


