题目内容
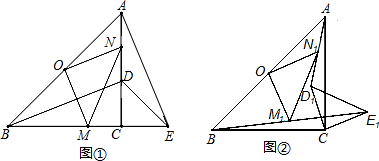
10.画△ABC,使AB=8,AC=6,AD是BC边上的中线,将△ADC绕点D旋转180°,并画出图形,量一量AD的长,想一想,AD的取值在什么范围内?由此归纳出三角形一边上的中线的取值应满足什么条件,并解答.已知三角形的两边长分别为6和x,第三边上的中线长为4,求x的取值范围.分析 根据旋转的性质得AD=ED,BE=AC,所以当AB=8,AC=6时,在△ABE中,AE=2AD,BE=AC=6,利用三角形三边的关系得到8-6<2AD<8+6,再解不等式组即得到AD的取值范围,由此归纳出三角形一边上的中线的取值应满足的条件;若三角形的两边长分别为6和x,第三边上的中线长为4,利用上述结论有:当x≤6,则6-x<2•4<6+x;当x>6,则x-6<2•4<6+x,然后分别解不等式组,最后确定x的取值范围.
解答 解: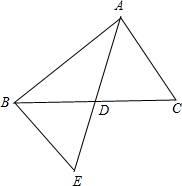 如图,∵AD是BC边上的中线,
如图,∵AD是BC边上的中线,
∴BD=CD,
∴△ADC绕点D旋转180°得到△EDB,
∴AD=ED,BE=AC,
当AB=8,AC=6时,
在△ABE中,AE=2AD,BE=AC=6,
∴8-6<2AD<8+6,
∴AD的取值范围为1<AD<7,
由此归纳出三角形一边上的中线的取值应满足的条件为:三角形一边上的中线大于另两边差的一半小于另两边的和的一半;
若三角形的两边长分别为6和x,第三边上的中线长为4,
当x≤6,则6-x<2•4<6+x,解得2<x≤6;
当x>6,则x-6<2•4<6+x,解得6<x<14,
所以x的范围为2<x<14.
点评 本题考查了作图:旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了三角形三边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.为了了解某校七年级考数学科各分数段成绩分布情况,从中抽取200名考生的段考数学成绩进行统计分析,在这个问题中,样本是( )
| A. | 200 | |
| B. | 被抽取的200名学生 | |
| C. | 被抽取的200名考生的段考数学成绩 | |
| D. | 某校七年级段考数学成绩 |
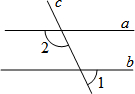 如图,直线c与a、b都相交,a∥b,如果∠2=110°,那么∠1=70°.
如图,直线c与a、b都相交,a∥b,如果∠2=110°,那么∠1=70°.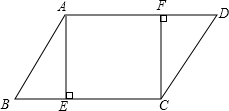 如图所示,在四边形ABCD中,AE⊥BC于E,CF⊥AD于F,如果AD∥BC且AF=CE,那么四边形AECF是平行四边形?说明理由.
如图所示,在四边形ABCD中,AE⊥BC于E,CF⊥AD于F,如果AD∥BC且AF=CE,那么四边形AECF是平行四边形?说明理由.