题目内容
3.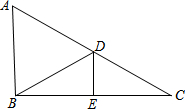 如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )
如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )| A. | 58 | B. | 59 | C. | 61 | D. | 62 |
分析 根据线段垂直平分线的性质、角平分线的定义得到∠1=∠2=∠3,求出∠4和∠C,根据三角形内角和定理计算即可.
解答 解:∵BD是∠ADE的角平分线,
∴∠1=∠2,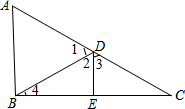
∵DE是BC的中垂线,
∴∠2=∠3,
∴∠1=∠2=∠3,又∠1+∠2+∠3=180°,
∴∠1=∠2=∠3=60°,
∴∠4=∠C=90°-60°=30°,
∴∠ABD=180°-∠A-∠4-∠C=180°-58°-30°-30°=62°.
故选:D.
点评 本题考查的是线段垂直平分线的性质、角平分线的定义以及三角形内角和定理的应用,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
14.下列函数中,满足y的值随x的值增大而增大的是( )
| A. | y=-2x | B. | y=3x-1 | C. | y=$\frac{1}{x}$ | D. | y=x2 |
11.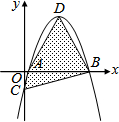 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
8.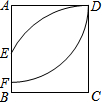 如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
 如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )| A. | 2 | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{7}{3}$ |
15.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对重庆市居民日平均用水量的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对重庆新闻频道“天天630”栏目收视率的调查 | |
| D. | 对某校九年级(1)班同学的身高情况的调查 |
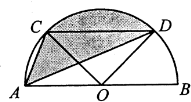
12.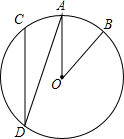 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )| A. | 40° | B. | 30° | C. | 20° | D. | 15° |