题目内容
13.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定满足( )| A. | 对角线相等 | B. | 对角线互相平分 | ||
| C. | 对角线互相垂直 | D. | 对角线相等且互相平分 |
分析 根据三角形的中位线定理得到EH∥FG,EF=FG,EF=$\frac{1}{2}$BD,要是四边形为菱形,得出EF=EH,即可得到答案.
解答 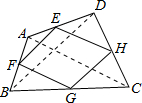 解:∵E,F,G,H分别是边AD,DC,CB,AB的中点,
解:∵E,F,G,H分别是边AD,DC,CB,AB的中点,
∴EH=$\frac{1}{2}$AC,EH∥AC,FG=$\frac{1}{2}$AC,FG∥AC,EF=$\frac{1}{2}$BD,
∴EH∥FG,EF=FG,
∴四边形EFGH是平行四边形,
假设AC=BD,
∵EH=$\frac{1}{2}$AC,EF=$\frac{1}{2}$BD,
则EF=EH,
∴平行四边形EFGH是菱形,
即只有具备AC=BD即可推出四边形是菱形,
故选A.
点评 本题主要考查对菱形的判定,三角形的中位线定理,平行四边形的判定等知识点的理解和掌握,灵活运用性质进行推理是解此题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
3. 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | OA=OC |
2.如果把分式$\frac{2x}{{x}^{2}+{y}^{2}}$中的x和y都扩大3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小6倍 | D. | 缩小3倍 |
 如图,在△ABC中,∠ACB=90°,AB=10cm,BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AC运动,当t=5s或6s或$\frac{25}{6}$s时,△ABD为等腰三角形.
如图,在△ABC中,∠ACB=90°,AB=10cm,BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AC运动,当t=5s或6s或$\frac{25}{6}$s时,△ABD为等腰三角形.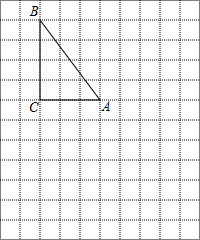 在右边网格图中,每个小正方形的边长均为1个单位长度,△ABC为直角三角形,∠C=90°,AC=3,BC=4.
在右边网格图中,每个小正方形的边长均为1个单位长度,△ABC为直角三角形,∠C=90°,AC=3,BC=4.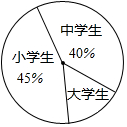 为了了解某地区大、中、小学生课外阅读情况,教育部门从这三类学生群体中共抽取了4200名学生进行调查,各类学生所占比例如图所示,则大学生共调查了630人.
为了了解某地区大、中、小学生课外阅读情况,教育部门从这三类学生群体中共抽取了4200名学生进行调查,各类学生所占比例如图所示,则大学生共调查了630人. 抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3)
抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3)