题目内容
4. 如图,在△ABC中,∠ACB=90°,AB=10cm,BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AC运动,当t=5s或6s或$\frac{25}{6}$s时,△ABD为等腰三角形.
如图,在△ABC中,∠ACB=90°,AB=10cm,BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AC运动,当t=5s或6s或$\frac{25}{6}$s时,△ABD为等腰三角形.
分析 由题意可知AP=2t,当AB=AP时,有2t=10;当AB=BP时,则可知AC=CP,则AP=12,即2t=12;当AP=BP时,CP=2t-6,BP=2t,在Rt△BPC中,由勾股定理可得BC2+CP2=BP2,可得到关于t的方程,分别求得t即可.
解答 解:由题意可知AP=2t,
当AB=AP时,有2t=10,解得t=5;
当AB=BP时,则可知AC=CP,则AP=12,即2t=12,解得t=6;
当AP=BP时,CP=2t-6,BP=2t,在Rt△BPC中,由勾股定理可得BC2+CP2=BP2,
即64+(2t-6)2=4t2,解得t=$\frac{25}{6}$;
综上可知t的值为5s或6s或$\frac{25}{6}$s.
故答案为:5s或6s或$\frac{25}{6}$s.
点评 本题主要考查等腰三角形的性质,由条件分三种情况分别得到关于t的方程是解题的关键,利用时间表示出AP,即化动为静是解题的技巧.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.已知点P(m,1)在第二象限,则点Q(-m,-3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定满足( )
| A. | 对角线相等 | B. | 对角线互相平分 | ||
| C. | 对角线互相垂直 | D. | 对角线相等且互相平分 |
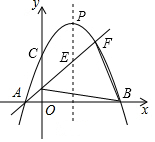 如图,二次函数y=-ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.
如图,二次函数y=-ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF. 如图,一次函数y=kx+1的图形经过点A(1,2),且与x轴相交于点B,若点P是y轴上一点,且满足△APB是等腰三角形,则点P的坐标可以是(0,2+$\sqrt{7}$),(0,2-$\sqrt{7}$),(0,$\sqrt{7}$),(0,-$\sqrt{7}$).
如图,一次函数y=kx+1的图形经过点A(1,2),且与x轴相交于点B,若点P是y轴上一点,且满足△APB是等腰三角形,则点P的坐标可以是(0,2+$\sqrt{7}$),(0,2-$\sqrt{7}$),(0,$\sqrt{7}$),(0,-$\sqrt{7}$).