题目内容
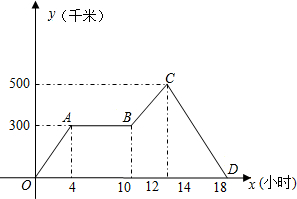 王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空:
王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空:(1)王老师修车用了
(2)学校到开会地点的距离是
(3)快客的平均速度是
(4)图象BC的函数解析式为
考点:一次函数的应用
专题:
分析:(1)修车时,离学校的路程不变;
(2)图中的纵坐标表示学校到开会地点的距离;
(3)由路程÷时间=速度进行计算;
(4)利用待定系数法求得该直线方程.
(2)图中的纵坐标表示学校到开会地点的距离;
(3)由路程÷时间=速度进行计算;
(4)利用待定系数法求得该直线方程.
解答: 解:(1)如图,王老师修车时间是从4时到10时,共用了:10-4=6(小时);
解:(1)如图,王老师修车时间是从4时到10时,共用了:10-4=6(小时);
(2)根据图示知,学校到开会地点的距离是 500千米;
(3)快客的平均速度是:500÷5=100(千米/时);
(4)设直线BC的解析式为y=kx+b(k≠0).
由图示知,B(10,300),(13,500),则
,
解之得
,
所以直线BC的解析式为:y=
x-
(10≤x≤13).
故答案是:(1)6;(2)500;(3)100;(4)y=
x-
.
 解:(1)如图,王老师修车时间是从4时到10时,共用了:10-4=6(小时);
解:(1)如图,王老师修车时间是从4时到10时,共用了:10-4=6(小时);(2)根据图示知,学校到开会地点的距离是 500千米;
(3)快客的平均速度是:500÷5=100(千米/时);
(4)设直线BC的解析式为y=kx+b(k≠0).
由图示知,B(10,300),(13,500),则
|
解之得
|
所以直线BC的解析式为:y=
| 200 |
| 3 |
| 1100 |
| 3 |
故答案是:(1)6;(2)500;(3)100;(4)y=
| 200 |
| 3 |
| 1100 |
| 3 |
点评:本题考查了函数的图象以及待定系数法求函数的解析式,正确利用数形结合思想,把数值的大小转化为点的坐标之间的关系是关键.

练习册系列答案
相关题目
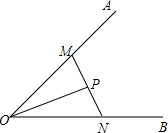 已知:在∠AOB的边OA、OB上分别取M、N两点,使OM=ON;连接MN,取MN的中点P,连接OP,证明:射线OP是∠AOB的平分线.
已知:在∠AOB的边OA、OB上分别取M、N两点,使OM=ON;连接MN,取MN的中点P,连接OP,证明:射线OP是∠AOB的平分线. 如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.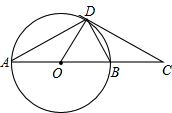 如图,AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.
如图,AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.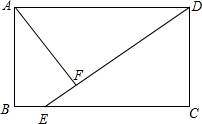 如图,在矩形ABCD中,点E在BC上,AF⊥DE于点F,且AF=3,CD=5,DE=15.求矩形ABCD的面积.
如图,在矩形ABCD中,点E在BC上,AF⊥DE于点F,且AF=3,CD=5,DE=15.求矩形ABCD的面积.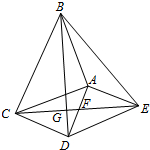 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中: