题目内容
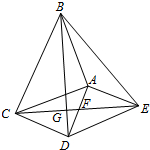 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:①BD=CE;②BD⊥CE;③△ADC是等腰直角三角形;④△AEC≌△AEB;⑤∠ADB=∠AEB
一定正确的结论有
考点:全等三角形的判定与性质,等腰直角三角形,平行四边形的性质
专题:
分析:根据等腰直角三角形的性质可得AB=AC,AD=AE,再求出∠BAD=∠CAE,然后利用“边角边”证明△AEC与△ADB全等,根据全等三角形的对应边相等可得BD=CE,判断出①正确;
全等三角形对应角相等可得∠DAB=∠EAC,再求出∠CBG+∠BCG=90°,然后求出BD⊥CE,判断出②正确;
根据平行四边形对称性可得△ADE和△DCA全等从而判断出③正确;
求出∠CAE=∠BAE=135°,然后利用“边角边”证明△AEC和△AEB全等,判断出④正确;
根据全等三角形对应角相等可得∠ADB=∠ACE=∠AEB,判断出⑤正确.
全等三角形对应角相等可得∠DAB=∠EAC,再求出∠CBG+∠BCG=90°,然后求出BD⊥CE,判断出②正确;
根据平行四边形对称性可得△ADE和△DCA全等从而判断出③正确;
求出∠CAE=∠BAE=135°,然后利用“边角边”证明△AEC和△AEB全等,判断出④正确;
根据全等三角形对应角相等可得∠ADB=∠ACE=∠AEB,判断出⑤正确.
解答:解:∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∵∠BAD=90°+∠CAD,
∠CAE=90°+∠CAD,
∴∠BAD=∠CAE,
在△AEC与△ADB中,
,
∴△AEC≌△ADB(SAS),
∴BD=CE,故①正确;
∠DAB=∠EAC,
∴∠CBG+∠BCG=90°,
∴BD⊥CE,故②正确;
∵四边形ACDE是平行四边形,
∴△ADE≌△DCA,
∴△ADC是等腰直角三角形,故③正确;
∵∠CAE=90°+∠CAD=135°,
∠BAE=360°-90°-135°=135°,
∴∠CAE=∠BAE=135°,
在△AEC和△AEB,
,
∴△AEC≌△AEB(SAS),故④正确;
∴△AEC≌△ADB≌△AEB,
∴∠ADB=∠AEB,故⑤正确;
综上所述,正确的结论有①②③④⑤.
故答案为:①②③④⑤.
∴AB=AC,AD=AE,
∵∠BAD=90°+∠CAD,
∠CAE=90°+∠CAD,
∴∠BAD=∠CAE,
在△AEC与△ADB中,
|
∴△AEC≌△ADB(SAS),
∴BD=CE,故①正确;
∠DAB=∠EAC,
∴∠CBG+∠BCG=90°,
∴BD⊥CE,故②正确;
∵四边形ACDE是平行四边形,
∴△ADE≌△DCA,
∴△ADC是等腰直角三角形,故③正确;
∵∠CAE=90°+∠CAD=135°,
∠BAE=360°-90°-135°=135°,
∴∠CAE=∠BAE=135°,
在△AEC和△AEB,
|
∴△AEC≌△AEB(SAS),故④正确;
∴△AEC≌△ADB≌△AEB,
∴∠ADB=∠AEB,故⑤正确;
综上所述,正确的结论有①②③④⑤.
故答案为:①②③④⑤.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,平行四边形的性质,熟记各性质是解题的关键,根据角的度数相等得到相等的角是证明④的关键.

练习册系列答案
相关题目
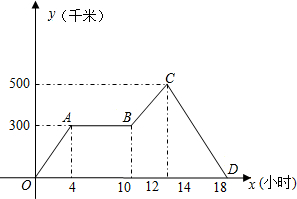 王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空:
王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空: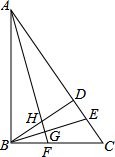 如图,在Rt△ABC中,∠ABC=90°,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.若∠BAC=30°,则
如图,在Rt△ABC中,∠ABC=90°,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.若∠BAC=30°,则