题目内容
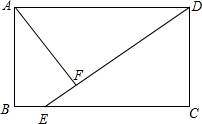如图，在矩形ABCD中，点E在BC上，AF⊥DE于点F，且AF=3，CD=5，DE=15．求矩形ABCD的面积．考点：矩形的性质
专题：
分析：由在矩形ABCD中，点E在BC上，AF⊥DE于点F，易证得△ADF∽△DEC，又由相似三角形的对应边成比例，求得AD的长，继而求得答案．
解答：解：∵四边形ABCD是矩形，
∴AD∥BC，∠C=90°，
∴∠ADF=∠CED，
∵AF⊥DE，
∴∠AFD=∠C=90°，
∴△ADF∽△DEC，
∴
=
，
∵AF=3，CD=5，DE=15，
∴
=
，
∴AD=9，
∴矩形ABCD的面积为：AD•CD=45．
∴AD∥BC，∠C=90°，
∴∠ADF=∠CED，
∵AF⊥DE，
∴∠AFD=∠C=90°，
∴△ADF∽△DEC，
∴
| AD |
| DE |
| AF |
| CD |
∵AF=3，CD=5，DE=15，
∴
| AD |
| 15 |
| 3 |
| 5 |
∴AD=9，
∴矩形ABCD的面积为：AD•CD=45．
点评：此题考查了相似三角形的判定与性质以及矩形的性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D、C分别落在D′、C′的位置上，若∠EFG=55°，求∠AEG和∠EGB的度数．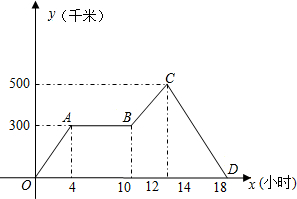
王老师从学校乘汽车去城里开会，4小时后，汽车出现故障，修理一段时间后继续走，又过了3个小时到达开会地点，而此时接到紧急通知，立马乘快客赶回学校．根据图中信息填空：