题目内容
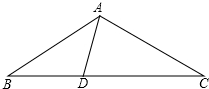 在△ABC中,AB=AC=6,∠BAC=108°,点D在边BC上,∠BAD=36°.
在△ABC中,AB=AC=6,∠BAC=108°,点D在边BC上,∠BAD=36°.(1)求证:△BAD∽△BCA;
(2)求AD的长.
考点:相似三角形的判定与性质
专题:
分析:(1)证明∠B=∠C=36°;结合∠BAD=36°,得到△BAD∽△BCA.
(2)证明BD=AD(设为λ);证明DC=AC=6;由△BAD∽△BCA,得到
=
,即
=
,求出λ=3
-3,即可解决问题.
(2)证明BD=AD(设为λ);证明DC=AC=6;由△BAD∽△BCA,得到
| AD |
| AB |
| AB |
| AC |
| λ |
| 6 |
| 6 |
| λ+6 |
| 5 |
解答: 解:(1)∵AB=AC=6,∠BAC=108°,
解:(1)∵AB=AC=6,∠BAC=108°,
∴∠B=∠C=
=36°;
∵∠BAD=36°,
∴△BAD∽△BCA.
(2)∵∠B=∠BAD,
∴BD=AD(设为λ);
∵∠ADC=∠B+∠BAD=72°,∠DAC=108°-36°=72°,
∴∠ADC=∠DAC,DC=AC=6;
∵△BAD∽△BCA,
∴
=
,即
=
,
解得:λ=3
-3,
即AD的长=3
-3.
 解:(1)∵AB=AC=6,∠BAC=108°,
解:(1)∵AB=AC=6,∠BAC=108°,∴∠B=∠C=
| 180°-108° |
| 2 |
∵∠BAD=36°,
∴△BAD∽△BCA.
(2)∵∠B=∠BAD,
∴BD=AD(设为λ);
∵∠ADC=∠B+∠BAD=72°,∠DAC=108°-36°=72°,
∴∠ADC=∠DAC,DC=AC=6;
∵△BAD∽△BCA,
∴
| AD |
| AB |
| AB |
| AC |
| λ |
| 6 |
| 6 |
| λ+6 |
解得:λ=3
| 5 |
即AD的长=3
| 5 |
点评:该题主要考查了相似三角形的判定及其性质、等腰三角形的判定等几何知识点及其应用问题;解题的关键是牢固掌握相似三角形的判定及其性质、等腰三角形的判定等几何知识点.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
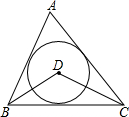 如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )
如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )| A、110° | B、120° |
| C、130° | D、140° |
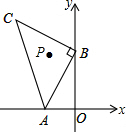 如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC.
如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC. 如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由.
如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由.
 如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?