题目内容
已知直线AB:y=-
x+3与抛物线y=
x2交于A,B两点,在直线AB下方的抛物线上求点P,使△ABP的面积等于5.
| 1 |
| 2 |
| 1 |
| 2 |
考点:二次函数的性质
专题:
分析:可联立两解析式可求得A、B两点的坐标,分别过A、B两点作x轴的垂线,分别交x轴于点C、D,过P作PE⊥x轴于点E,设出P点坐标,可分别表示出梯形ABDC、梯形BDEP和梯形APEC的面积,可表示出△ABP的面积,得到方程可求得P点坐标.
解答:解:联立直线AB和抛物线解析式可得
,
解得
或
,
则A(-3,
),B(2,2),
设P点坐标为(x,
x2),
分别过点A、B、P作x轴的垂直,垂足分别为C、D、E,如图,
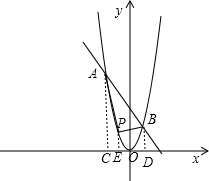
∴AC=
,PE=
x2,BD=2,DE=2-x,CE=x+3,CD=5,
∴S梯形ABDC=
(BD+AC)CD=
×(2+
)×5=
,
S梯形BDEP=
(BD+PE)DE=
(2+
x2)(2-x),
S梯形ACEP=
(PE+AC)CE=
(
x2+
)(x+3),
∵S△ABP=S梯形ABDC-S梯形BDEP-S梯形ACEP,
∴
-
(2+
x2)(2-x)-
(
x2+
)(x+3)=5,
整理可得x2+x-2=0,解得x=-2或x=1,
∴P点坐标为(-2,2)或(1,
).
|
解得
|
|
则A(-3,
| 9 |
| 2 |
设P点坐标为(x,
| 1 |
| 2 |
分别过点A、B、P作x轴的垂直,垂足分别为C、D、E,如图,

∴AC=
| 9 |
| 2 |
| 1 |
| 2 |
∴S梯形ABDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 65 |
| 4 |
S梯形BDEP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S梯形ACEP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∵S△ABP=S梯形ABDC-S梯形BDEP-S梯形ACEP,
∴
| 65 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
整理可得x2+x-2=0,解得x=-2或x=1,
∴P点坐标为(-2,2)或(1,
| 1 |
| 2 |
点评:本题主要考查抛物线与直线的交点,求得交点的坐标用P点的坐标表示出△ABP的面积是解题的关键.

练习册系列答案
相关题目
若a>0且ax=2,ay=3,则ax+y的值为( )
| A、6 | ||
| B、5 | ||
| C、-1 | ||
D、
|
把20500000用科学记数法表示为( )
| A、20.5×106 |
| B、0.205×108 |
| C、205×105 |
| D、2.05×107 |
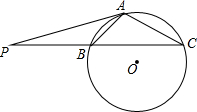 如图,P、B、C三点共线,⊙O经过B、C两点,A是⊙O上一点,连接PA,且∠PAB=∠C,PA=5,PB=3.
如图,P、B、C三点共线,⊙O经过B、C两点,A是⊙O上一点,连接PA,且∠PAB=∠C,PA=5,PB=3.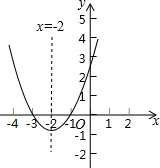 已知二次函数y=x2+4x+3,回答下列问题:
已知二次函数y=x2+4x+3,回答下列问题: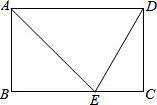 已知在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求证矩形的周长及对角线的长.
已知在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求证矩形的周长及对角线的长.