题目内容
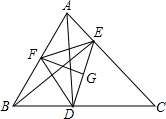 在△ABC中,AD⊥BC于点D,BE⊥AC于点E,F是AB的中点,FG⊥DE于点G,求证:∠DFG=∠EFG.
在△ABC中,AD⊥BC于点D,BE⊥AC于点E,F是AB的中点,FG⊥DE于点G,求证:∠DFG=∠EFG.考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:证明题
分析:利用直角三角形斜边上的中线等于斜边的一边得到FD=FE=
AB.然后由等腰三角形“三线合一”的性质证得结论.
| 1 |
| 2 |
解答: 证明:∵AD⊥BC,BE⊥AC,F是AB的中点,
证明:∵AD⊥BC,BE⊥AC,F是AB的中点,
∴FD=FE=
AB.
又∵FG⊥DE,
∴∠DFG=∠EFG.
 证明:∵AD⊥BC,BE⊥AC,F是AB的中点,
证明:∵AD⊥BC,BE⊥AC,F是AB的中点,∴FD=FE=
| 1 |
| 2 |
又∵FG⊥DE,
∴∠DFG=∠EFG.
点评:本题考查了直角三角形斜边上的中线和等腰三角形的判定与性质.利用“在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点)
”得到FD=FE是解题的关键.
”得到FD=FE是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
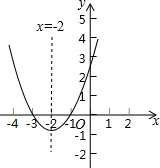 已知二次函数y=x2+4x+3,回答下列问题:
已知二次函数y=x2+4x+3,回答下列问题: